Реализация кубической кривой Безье в C
Что такое кривая Безье?
Таким образом, кривая Безье - это математически определенная кривая, используемая в двухмерных графических приложениях, таких как abode Illustrator, Inkscape и т. Д. Кривая определяется четырьмя точками: исходным положением и конечным положением, то есть P0 и P3 соответственно (которые называются «якорями»). ) и две отдельные средние точки, то есть P1 и P2 (которые называются «ручками») в нашем примере. Кривые Безье часто используются в компьютерной графике, анимации, моделировании и т. Д.
Как математически представить кривые Безье?
Кривые Безье могут быть построены под контролем других точек. Приблизительные касательные с использованием контрольных точек используются для построения кривой. Кривая Безье математически может быть представлена как - 
Где 
- множество точек и 
представляет полиномы Бернштейна, то есть функцию смешивания, которые задаются - 
Где n - порядок полиномов, i - индекс, а u / t - переменная, имеющая от 0 до 1 .
Давайте математически определим нашу кубическую кривую Безье.
Итак, идентификатор кривой Безье определяется набором контрольных точек. 
к 
где n называется его порядком (n = 1 для линейного, n = 2 для квадратичного и т. д.). Первая и последняя контрольные точки всегда являются конечными точками кривой; однако промежуточные контрольные точки (если они есть) обычно не лежат на кривой.
Для кубической кривой Безье порядок (n) полинома равен 3 , индекс (i) изменяется от i = 0 до i = n, т.е. 3 и u будет варьироваться от 
.
Функция кубической кривой Безье определяется как:
Функция наложения кубической кривой Безье определяется как:
Так 
а также 
Теперь, 
Таким образом, мы вычислим кривую x и y в пикселях, увеличивая значение u на 0,0001 .
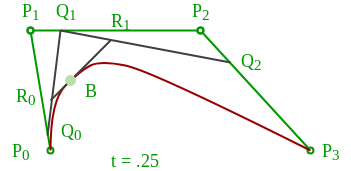
Построение кубической кривой Безье
Свойства кривых Безье
1. Они всегда проходят через первую и последнюю контрольные точки.
2. Они содержатся в выпуклой оболочке своих определяющих контрольных точек.
3. Степень полинома, определяющего сегмент кривой, на единицу меньше количества определяющих точек многоугольника. Следовательно, для 4 контрольных точек степень полинома равна 3, т.е. кубический полином.
4. Кривая Безье обычно повторяет форму определяющего многоугольника.
5. Направление касательного вектора в конечных точках такое же, как у вектора, определенного первым и последним отрезками.
6. Кривые Безье демонстрируют глобальный контроль: перемещение контрольной точки изменяет форму всей кривой.
ПРИМЕЧАНИЕ . Следующая реализация использует библиотеку SDL для рисования пикселей на экране. Если вы используете систему Debian, например, ubuntu, просто запускает следующую команду для установки библиотеки SDL.
Пример: У нас есть четыре контрольных точки B 0 [1,0], B 1 [2,2], B 2 [6,3], B 3 [8,2], поэтому определите пять точек, которые лежат на curve также нарисуйте кривую на графике.
Ответ: Данная кривая имеет четыре контрольных точки, следовательно, это кубическая кривая Безье. Итак, параметрическое уравнение кубической кривой Безье имеет вид
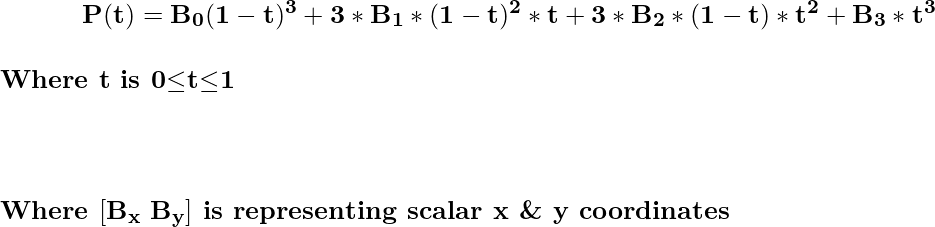
теперь подставьте контрольные точки в приведенное выше уравнение, чтобы получить,
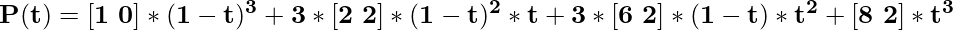
Предположим, что пять различных значений t равны {0, 0,2, 0,5, 0,7, 1}.
Итак, при t = 0 координата будет,
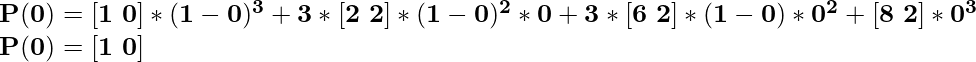
Итак, при t = 0,2 координата будет
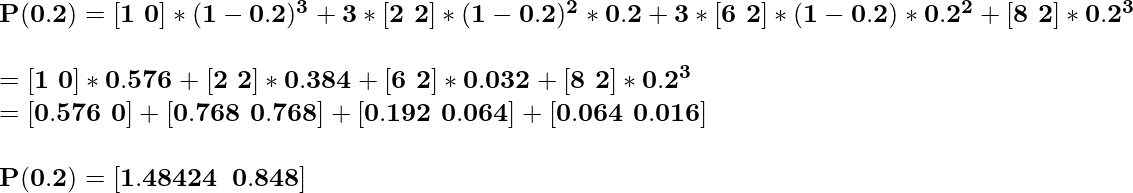
Итак, для t = 0,5 координата будет,
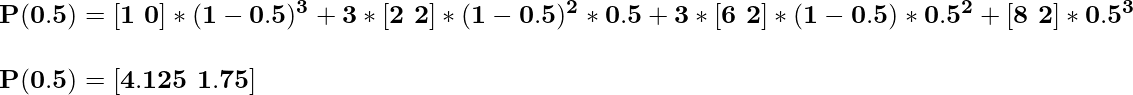
Итак, при t = 0,7 координата будет
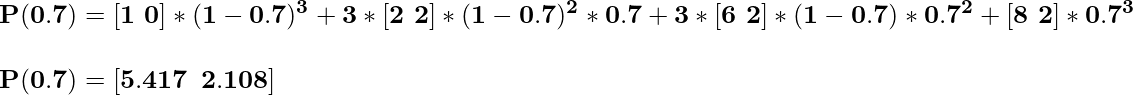
Итак, для t = 1.0 координата будет,
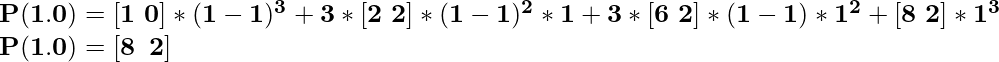
Рисунок 1
Недостатки кривой Безье :
а) Степень кривой Безье зависит от количества контрольных точек, связанных с соответствующей кривой, поскольку количество контрольных точек увеличивается, полиномиальная степень уравнения кривой также увеличивается, что делает уравнение кривой очень сложным и трудным для решения.
Степень изгиба = нет. контрольных точек - 1
б) Одним из основных недостатков использования кривой Безье является то, что они придают кривой глобальный контроль. Это означает, что при изменении относительного положения кривой изменяется вся форма кривой. Это делает его менее удобным в использовании.
При изменении относительного положения любой из контрольных точек изменяется вся форма кривой:
c) Еще одна проблема с Безье заключается в том, что его функция смешивания никогда не достигает нуля ни для одного параметра, независимо от степени кривой.
sudo apt-get install libsdl2-dev
Для построения использовать
gcc имя_файла.c -lSDL2 -lm
C
// C program to implement// Cubic Bezier Curve/* install SDL library for running thing code*//* install by using this commamnd line : sudo apt-get install libsdl2-dev *//* run this code using command : gcc fileName.c -lSDL2 -lm*/#include<stdio.h>#include<stdlib.h>#include<math.h>#include<SDL2/SDL.h>SDL_Window* window = NULL;SDL_Renderer* renderer = NULL;int mousePosX , mousePosY ;int xnew , ynew ;/*Function to draw all other 7 pixels present at symmetric position*/void drawCircle(int xc, int yc, int x, int y){ SDL_RenderDrawPoint(renderer,xc+x,yc+y) ; SDL_RenderDrawPoint(renderer,xc-x,yc+y); SDL_RenderDrawPoint(renderer,xc+x,yc-y); SDL_RenderDrawPoint(renderer,xc-x,yc-y); SDL_RenderDrawPoint(renderer,xc+y,yc+x); SDL_RenderDrawPoint(renderer,xc-y,yc+x); SDL_RenderDrawPoint(renderer,xc+y,yc-x); SDL_RenderDrawPoint(renderer,xc-y,yc-x);}/*Function for circle-generation using Bresenham"s algorithm */void circleBres(int xc, int yc, int r){ int x = 0, y = r; int d = 3 - 2 * r; while (y >= x) { /*for each pixel we will draw all eight pixels */ drawCircle(xc, yc, x, y); x++; /*check for decision parameter and correspondingly update d, x, y*/ if (d > 0) { y--; d = d + 4 * (x - y) + 10; } else d = d + 4 * x + 6; drawCircle(xc, yc, x, y); }}/* Function that take input as Control Point x_coordinates andControl Point y_coordinates and draw bezier curve */void bezierCurve(int x[] , int y[]){ double xu = 0.0 , yu = 0.0 , u = 0.0 ; int i = 0 ; for(u = 0.0 ; u <= 1.0 ; u += 0.0001) { xu = pow(1-u,3)*x[0]+3*u*pow(1-u,2)*x[1]+3*pow(u,2)*(1-u)*x[2] +pow(u,3)*x[3]; yu = pow(1-u,3)*y[0]+3*u*pow(1-u,2)*y[1]+3*pow(u,2)*(1-u)*y[2] +pow(u,3)*y[3]; SDL_RenderDrawPoint(renderer , (int)xu , (int)yu) ; }}int main(int argc, char* argv[]){ /*initialize sdl*/ if (SDL_Init(SDL_INIT_EVERYTHING) == 0) { /* This function is used to create a window and default renderer. int SDL_CreateWindowAndRenderer(int width ,int height ,Uint32 window_flags ,SDL_Window** window ,SDL_Renderer** renderer) return 0 on success and -1 on error */ if(SDL_CreateWindowAndRenderer(640, 480, 0, &window, &renderer) == 0) { SDL_bool done = SDL_FALSE; int i = 0 ; int x[4] , y[4] , flagDrawn = 0 ; while (!done) { SDL_Event event; /*set background color to black*/ SDL_SetRenderDrawColor(renderer, 0, 0, 0, SDL_ALPHA_OPAQUE); SDL_RenderClear(renderer); /*set draw color to white*/ SDL_SetRenderDrawColor(renderer, 255, 255, 255, SDL_ALPHA_OPAQUE); /* We are drawing cubic bezier curve which has four control points */ if(i==4) { bezierCurve(x , y) ; flagDrawn = 1 ; } /*grey color circle to encircle control Point P0*/ SDL_SetRenderDrawColor(renderer, 128, 128, 128, SDL_ALPHA_OPAQUE); circleBres(x[0] , y[0] , 8) ; /*Red Line between control Point P0 & P1*/ SDL_SetRenderDrawColor(renderer, 255, 0, 0, SDL_ALPHA_OPAQUE); SDL_RenderDrawLine(renderer , x[0] , y[0] , x[1] , y[1]) ; /*grey color circle to encircle control Point P1*/ SDL_SetRenderDrawColor(renderer, 128, 128, 128, SDL_ALPHA_OPAQUE); circleBres(x[1] , y[1] , 8) ; /*Red Line between control Point P1 & P2*/ SDL_SetRenderDrawColor(renderer, 255, 0, 0, SDL_ALPHA_OPAQUE); SDL_RenderDrawLine(renderer , x[1] , y[1] , x[2] , y[2]) ; /*grey color circle to encircle control Point P2*/ SDL_SetRenderDrawColor(renderer, 128, 128, 128, SDL_ALPHA_OPAQUE); circleBres(x[2] , y[2] , 8) ; /*Red Line between control Point P2 & P3*/ SDL_SetRenderDrawColor(renderer, 255, 0, 0, SDL_ALPHA_OPAQUE); SDL_RenderDrawLine(renderer , x[2] , y[2] , x[3] , y[3]) ; /*grey color circle to encircle control Point P3*/ SDL_SetRenderDrawColor(renderer, 128, 128, 128, SDL_ALPHA_OPAQUE); circleBres(x[3] , y[3] , 8) ; /*We are Polling SDL events*/ if (SDL_PollEvent(&event)) { /* if window cross button clicked then quit from window */ if (event.type == SDL_QUIT) { done = SDL_TRUE; } /*Mouse Button is Down */ if(event.type == SDL_MOUSEBUTTONDOWN) { /*If left mouse button down then store that point as control point*/ if(event.button.button == SDL_BUTTON_LEFT) { /*store only four points because of cubic bezier curve*/ if(i < 4) { printf("Control Point(P%d):(%d,%d)
" ,i,mousePosX,mousePosY) ; /*Storing Mouse x and y positions in our x and y coordinate array */ x[i] = mousePosX ; y[i] = mousePosY ; i++ ; } } } /*Mouse is in motion*/ if(event.type == SDL_MOUSEMOTION) { /*get x and y positions from motion of mouse*/ xnew = event.motion.x ; ynew = event.motion.y ; int j ; /* change coordinates of control point after bezier curve has been drawn */ if(flagDrawn == 1) { for(j = 0 ; j < i ; j++) { /*Check mouse position if in b/w circle then change position of that control point to mouse new position which are coming from mouse motion*/ if((float)sqrt(abs(xnew-x[j]) * abs(xnew-x[j]) + abs(ynew-y[j]) * abs(ynew-y[j])) < 8.0) { /*change coordinate of jth control point*/ x[j] = xnew ; y[j] = ynew ; printf("Changed Control Point(P%d):(%d,%d)
" ,j,xnew,ynew) ; } } } /*updating mouse positions to positions coming from motion*/ mousePosX = xnew ; mousePosY = ynew ; } } /*show the window*/ SDL_RenderPresent(renderer); } } /*Destroy the renderer and window*/ if (renderer) { SDL_DestroyRenderer(renderer); } if (window) { SDL_DestroyWindow(window); } } /*clean up SDL*/ SDL_Quit(); return 0;} |
Output
Переместите мышь, когда положение мыши находится в черно-белом круге, тогда будет изменена только форма кривой
Использованная литература:
https://en.wikipedia.org/wiki/B%C3%A9zier_curve
https://www.tutorialspoint.com/computer_graphics/computer_graphics_curves.htm
http://www.math.ucla.edu/~baker/149.1.02w/handouts/bb_bezier.pdf
Автор статьи: Палканш Ханделвал.
Вниманию читателя! Не прекращайте учиться сейчас. Получите все важные математические концепции для соревновательного программирования с курсом Essential Maths for CP по доступной для студентов цене. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .