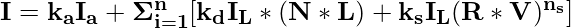Модель Фонга (зеркальное отражение) в компьютерной графике

Условие — базовые модели освещения

Модель отражения Фонга:
Когда мы смотрим на освещенные блестящие поверхности, такие как блестящие поверхности, полированные металлические листы, яблоко и т. д., мы обнаруживаем своего рода яркое пятно в определенных точках обзора. Это явление называется зеркальным отражением.

Посмотрите на следующий рисунок:

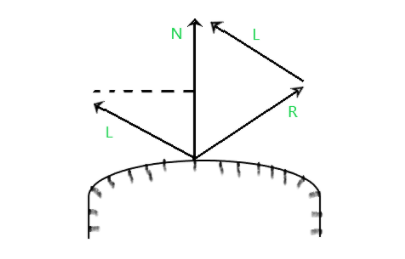
N = Normal vector
L = Point light source
V = Viewing direction
R = is representing the unit vector directed towards the ideal specular reflection
∅ = Viewing angle relative to the specular reflection direction R.
θ = Angle made by L & R with N.

Для идеальных поверхностей отражателя (идеальное зеркало) падающий свет отражается только в направлении зеркального отражения. Таким образом, в этом случае мы могли бы видеть отраженный свет, когда векторы V и R совпадают (угол обзора (∅ = 0)) .

Блестящая поверхность имеет узкий диапазон зеркального отражения, тогда как матовая поверхность имеет более широкий диапазон отражения. Эмпирическая модель для расчета диапазона зеркального отражения, изобретенная Фонг Буй Туонгом, также известна как модель зеркального отражения Фонга . В этой модели интенсивность зеркального отражения прямо пропорциональна cos ^{n _s} (∅) . Диапазон угла ∅ может лежать в пределах 0 ≤ ∅ ≤ 1. Где _ns — параметр зеркального отражения , значение которого определяется типом отображаемой поверхности. Значение _ns для более ярких (блестящих) поверхностей может быть 100 или больше, тогда как для тусклых поверхностей его значение равно 1 или меньше 1. Интенсивность зеркального отражения зависит от свойств объекта (материала) поверхности и угла падения света. падение, а также другие факторы, такие как поляризация и цвет падающего света.

Мы можем контролировать изменение интенсивности света через , зеркальное отражение, используя функцию спектрального отражения W(∅) для каждой поверхности. Где ∅ значение лежит в диапазоне 0 ≤ ∅ ≤ 1. В общем случае W(∅) имеет тенденцию к увеличению с увеличением угла падения, при ∅=90* W(90*)=1, и в этом случае все свет, падающий на поверхность материала, отражается. Итак, используя функцию спектрального отражения W(∅), мы можем записать модель зеркального отражения Фонга как:

Для поверхностей многих непрозрачных материалов зеркальные отражения почти постоянны для всех углов падения. Таким образом, в таком случае мы можем заменить W(∅) постоянным коэффициентом (Ks) , значение которого находится между 0 и 1 для каждой поверхности:

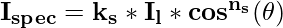
Since, V & R are unit vectors so, |V|=|R|=1 :
                          V * R = |V|*|R|*cos(θ)  , 
                          V * R = cos(θ)                                                                                 

Таким образом, мы можем записать только предыдущее уравнение как:

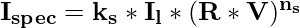
Здесь R можно вычислить путем проекции L на направление вектора нормали:

R + L = (2*N.L)*N
So, using the above equation specular-reflection vector is obtained,
R = (2*N.L)*N - L.

Комбинированные окружающие, диффузные и зеркальные отражения в модели Фонга могут быть представлены в виде следующего уравнения с несколькими источниками света:

Таким образом, для одноточечного источника света мы можем смоделировать комбинированные и зеркальные отражения от точки на освещенной поверхности следующим образом:

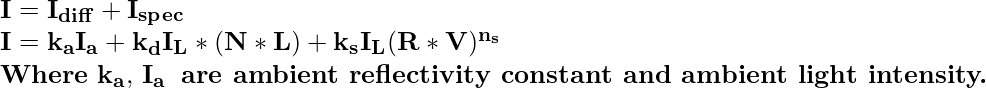
А для n точечных источников света уравнение будет таким: