Параметрическая и геометрическая непрерывность кривых в компьютерной графике

Условие: кривая B-сплайна, кривая Безье

Условие непрерывности показывает, насколько плавно кривая переходит от одного сегмента кривой к другому сегменту. Предположим, вам дана кривая, как показано ниже:

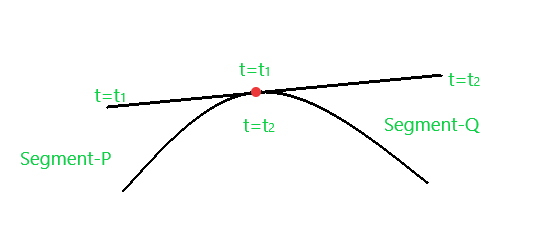
Существуют три вида параметрической непрерывности:

(a) Параметрическая непрерывность нулевого порядка (_C ⁰ ) : кривая называется параметрически непрерывной нулевого порядка, если оба сегмента кривой пересекаются в одной конечной точке.

                                        P(t2) =  Q(t1)

(b) Параметрическая непрерывность первого порядка (C ¹ ) : кривая называется параметрически непрерывной первого порядка, если она C ^o Continuous и производная первого порядка сегмента P в момент t=t ₂ равна первой- производная по порядку сегмента Q в момент t=t ₁ . Такие кривые имеют одну и ту же касательную в точке пересечения.

                                     P"(t2) = Q"(t1)

(c) Параметрическая непрерывность второго порядка (C ² ): кривая называется параметрически непрерывной второго порядка, если она является непрерывной C ⁰ и C ¹ и производная второго порядка отрезка P в момент t=t ₁ равна к производной второго порядка отрезка Q при t=t ₂ .

                                    P""(t2) = Q""(t1)

Геометрическая непрерывность : это альтернативный метод соединения двух сегментов кривой, где требуется параметрическое определение обоих сегментов, которые пропорциональны друг другу, а не равны друг другу.

(a) Геометрическая непрерывность нулевого порядка (G ^o ) : аналогично условию непрерывности параметрической кривой нулевого порядка.

                                         P(t2) =  Q(t1)

(b) Геометрическая непрерывность первого порядка (G ¹ ) : точка соединения между двумя точками называется непрерывной G ¹ , если координата обоих сегментов кривой непрерывна G ⁰ и выполняется следующее условие:

                                 P"(t2) =  k * Q"(t1)  for all x, y, z and k > 0.

(c) Геометрическая непрерывность второго порядка (G ² ) : точка соединения между двумя точками называется непрерывной G ² , если координаты обоих сегментов кривой являются непрерывными G ¹ и выполняются следующие условия:

                                P""(t2) =  k * Q""(t1)  for all x, y, z and k > 0.