Алгоритм Брезенхема для трехмерного рисования линий
Учитывая две трехмерные координаты, нам нужно найти точки на соединяющей их линии. Все точки имеют целые координаты.
Примеры:
Ввод: (-1, 1, 1), (5, 3, -1)
Выход: (-1, 1, 1), (0, 1, 1), (1, 2, 0),
(2, 2, 0), (3, 2, 0), (4, 3, -1),
(5, 3, -1)



 Ввод: (-7, 0, -3), (2, -5, -1)
Выход: (-7, 0, -3), (-6, -1, -3), (-5, -1, -3),
(-4, -2, -2), (-3, -2, -2), (-2, -3, -2),
(-1, -3, -2), (0, -4, -1), (1, -4, -1),
(2, -5, -1)
Ввод: (-7, 0, -3), (2, -5, -1)
Выход: (-7, 0, -3), (-6, -1, -3), (-5, -1, -3),
(-4, -2, -2), (-3, -2, -2), (-2, -3, -2),
(-1, -3, -2), (0, -4, -1), (1, -4, -1),
(2, -5, -1)
Алгоритм Брезенхема эффективен, поскольку он избегает арифметических операций с плавающей запятой. Как и в случае двухмерного рисования линии, мы используем переменную для хранения ошибки наклона, то есть ошибки наклона линии, которая строится от фактической геометрической линии. Как только эта погрешность наклона превышает допустимое значение, мы модифицируем цифру, чтобы устранить ошибку.
Ведущей осью линии, которая должна быть нанесена, является та, по которой линия проходит дальше всего, т.е. разница в координатах осей наибольшая. Таким образом, значения координат линейно увеличиваются на 1 вдоль ведущей оси, а переменная крутизны наклона используется для определения изменения значений координат другой оси.
В случае двухмерной линии мы используем одну переменную погрешности наклона, но в случае трехмерной линии нам нужны две (  ) из них для каждой из неведущих осей. Если текущая точка
) из них для каждой из неведущих осей. Если текущая точка  (x, y, z), а ведущая ось - положительная ось X, затем следующая точка
(x, y, z), а ведущая ось - положительная ось X, затем следующая точка  может быть
может быть
- (х + 1, у, г)
- (х + 1, у + 1, г)
- (х + 1, у, z + 1)
- (х + 1, у + 1, г + 1)

Значение переменных погрешности наклона определяется в соответствии со следующими уравнениями: 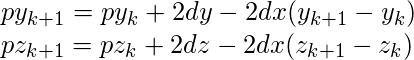
Начальное значение переменных погрешности наклона задается следующими уравнениями: - 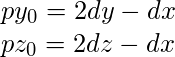
Здесь  обозначают разность координат двух конечных точек по осям X, Y, Z.
обозначают разность координат двух конечных точек по осям X, Y, Z.
Algorithm:-
- Input the two endpoints and store the initial point as
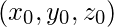
- Plot
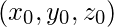
- Calculate constants
 and determine the driving axis by comparing
and determine the driving axis by comparing
the absolute values of
If abs(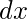 ) is maximum, then X-axis is the driving axis
) is maximum, then X-axis is the driving axis
If abs(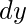 ) is maximum, then Y-axis is the driving axis
) is maximum, then Y-axis is the driving axis
If abs( ) is maximum, then Z-axis is the driving axis
) is maximum, then Z-axis is the driving axis - Let’s suppose that X-axis is the driving axis, then
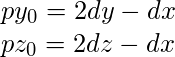
- At each
 along the line, starting at k = 0, check the following conditions
along the line, starting at k = 0, check the following conditions
and determine the next point:-- If
 AND
AND  , then
, then
plot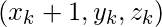 and
and
set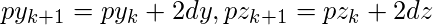
- Else If
 AND
AND  , then
, then
plot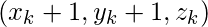 and
and
set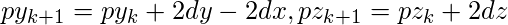
- Else If
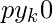 , then
, then
plot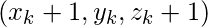 and
and
set
- Else then
plot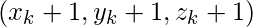 and
and
set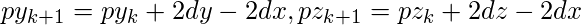 >
>
- If
- Repeat step 5
 times
times
Python3
# Python3 code for generating points on a 3-D line # using Bresenham"s Algorithm def Bresenham3D(x1, y1, z1, x2, y2, z2): ListOfPoints = [] ListOfPoints.append((x1, y1, z1)) dx = abs(x2 - x1) dy = abs(y2 - y1) dz = abs(z2 - z1) if (x2 > x1): xs = 1 else: xs = -1 if (y2 > y1): ys = 1 else: ys = -1 if (z2 > z1): zs = 1 else: zs = -1 # Driving axis is X-axis" if (dx >= dy and dx >= dz): p1 = 2 * dy - dx p2 = 2 * dz - dx while (x1 != x2): x1 += xs if (p1 >= 0): y1 += ys p1 -= 2 * dx if (p2 >= 0): z1 += zs p2 -= 2 * dx p1 += 2 * dy p2 += 2 * dz ListOfPoints.append((x1, y1, z1)) # Driving axis is Y-axis" elif (dy >= dx and dy >= dz): p1 = 2 * dx - dy p2 = 2 * dz - dy while (y1 != y2): y1 += ys if (p1 >= 0): x1 += xs p1 -= 2 * dy if (p2 >= 0): z1 += zs p2 -= 2 * dy p1 += 2 * dx p2 += 2 * dz ListOfPoints.append((x1, y1, z1)) # Driving axis is Z-axis" else: p1 = 2 * dy - dz p2 = 2 * dx - dz while (z1 != z2): z1 += zs if (p1 >= 0): y1 += ys p1 -= 2 * dz if (p2 >= 0): x1 += xs p2 -= 2 * dz p1 += 2 * dy p2 += 2 * dx ListOfPoints.append((x1, y1, z1)) return ListOfPoints def main(): (x1, y1, z1) = (-1, 1, 1) (x2, y2, z2) = (5, 3, -1) ListOfPoints = Bresenham3D(x1, y1, z1, x2, y2, z2) print(ListOfPoints) main() |
[(-1, 1, 1), (0, 1, 1), (1, 2, 0), (2, 2, 0), (3, 2, 0), (4, 3, -1), (5, 3, -1)]
Вниманию читателя! Не прекращайте учиться сейчас. Освойте все важные концепции DSA с помощью самостоятельного курса DSA по приемлемой для студентов цене и будьте готовы к работе в отрасли. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .
Если вы хотите посещать живые занятия с отраслевыми экспертами, пожалуйста, обращайтесь к Geeks Classes Live и Geeks Classes Live USA.