Z-Score в статистике

В этой статье мы собираемся обсудить следующие концепции,

• Что такое Z-Score?
• Формула Z-Score
• Как рассчитать Z-Score?
• Интерпретация Z-балла

Что такое Z-Score?

Z-оценка, также известная как стандартная оценка, дает нам представление о том, насколько далеко точка данных находится от среднего значения. Он показывает, на сколько стандартных отклонений элемент от среднего. Следовательно, Z-Score измеряется как стандартное отклонение от среднего. Например, стандартное отклонение 2 означает, что значение находится на 2 стандартных отклонения от среднего. Чтобы использовать z-показатель, нам необходимо знать среднее значение (μ), а также стандартное отклонение (σ).

Формула Z-Score

A z-score can be calculated using the following formula. 
 

z = (X – μ) / σ

where, 
z = Z-Score, 
X = The value of the element, 
μ = The population mean, and 
σ = The population standard deviation 
 

Как рассчитать Z-Score?

Обычно среднее значение совокупности ((μ), стандартное отклонение совокупности (σ) и наблюдаемое значение (x) приводятся в постановке задачи, и их замена в приведенном выше уравнении Z-оценки дает нам значение Z-Score. В зависимости от того, положительный или отрицательный данный Z-Score, можно использовать соответствующую положительную Z-таблицу или отрицательную Z-таблицу, доступную в Интернете или на обратной стороне вашего учебника статистики в приложении.

Пример:

Question: 
You take the GATE examination and score 500. The mean score for the GATE is 390 and the standard deviation is 45. How well did you score on the test compared to the average test taker? 

Solution: 
The following data is readily available in the above question statement 
Raw score/observed value = X = 500 
Mean score = μ = 390 
Standard deviation = σ = 45 

By applying the formula of z-score,  

z = (X – μ) / σ 
z = (500 – 390) / 45 
z = 110 / 45 = 2.44

This means that your z-score is 2.44. 

Since the Z-Score is positive 2.44, we will make use of the positive Z-Table. 

Now let’s take a look at Z Table (CC-BY) to know how well you scored compared to the other test-takers.

Follow the instruction below to find the probability from the table.

Here,  z-score = 2.44

1. Firstly, map the first two digits 2.4 on the Y-axis.
2. Then along the X-axis, map 0.04
3. Join both axes. The intersection of the two will provide you the Z-Score value you’re looking for

As a result, you will get the final value which is 0.99266.

Now, we need to compare how our original score of 500 on the GATE examination compares to the average score of the batch. To do that we need to convert the Z-Score into a percentage value.

0.99266 * 100 = 99.266%

Finally, you can say that you have performed well than almost 99% of other test-takers.

Интерпретация Z-балла

• Элемент с z-оценкой меньше 0 означает, что этот элемент меньше среднего.
• Элемент, имеющий z-оценку больше 0, означает, что этот элемент больше среднего.
• Элемент, имеющий z-оценку, равную 0, означает, что элемент равен среднему значению.
• Элемент, имеющий z-оценку, равную 1, означает, что элемент на 1 стандартное отклонение больше среднего; z-оценка равна 2, на 2 стандартных отклонения больше среднего и т. д.
• Элемент, имеющий z-оценку, равную -1, означает, что элемент на 1 стандартное отклонение меньше среднего; z-оценка равна -2, на 2 стандартных отклонения меньше среднего и т. д.
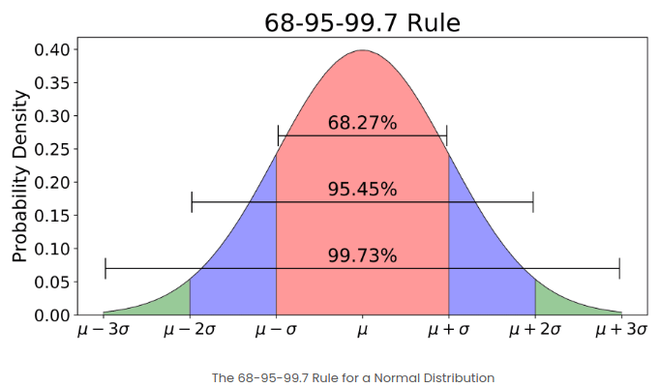
• Если количество элементов в данном наборе велико, то около 68% элементов имеют z-оценку от -1 до 1; около 95% имеют z-показатель от -2 до 2; около 99% имеют z-показатель от -3 до 3. Это называется эмпирическим правилом или правилом 68-95-99,7 и может быть продемонстрировано на изображении ниже.