Умножение матриц с 1 шагом MapReduce

Опубликовано: 18 Февраля, 2022

MapReduce - это метод, в котором огромная программа подразделяется на небольшие задачи и выполняется параллельно, чтобы ускорить вычисления, сэкономить время и в основном используется в распределенных системах. Он состоит из 2 важных частей:

Mapper: принимает необработанные данные и организует их в пары ключ-значение. Например, в словаре вы ищете слово «Данные», и его значение связано с «фактами и статистикой, собранными вместе для справки или анализа». Здесь ключ - это данные, а значение - это факты и статистика, собранные вместе для справки или анализа.
Редуктор: отвечает за параллельную обработку данных и за конечный результат.

Давайте рассмотрим пример умножения матриц для визуализации MapReduce. Рассмотрим следующую матрицу:

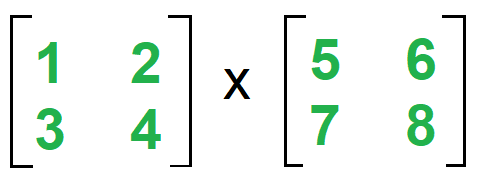
2 × 2 матрицы A и B

Здесь матрица A представляет собой матрицу 2 × 2, что означает количество строк (i) = 2 и количество столбцов (j) = 2. Матрица B также является матрицей 2 × 2, где количество строк (j) = 2 и количество столбцов (k) = 2. Каждая ячейка матрицы помечена как Aij и Bij. Бывший. элемент 3 в матрице A называется A21, т.е. 2-я строка 1-го столбца. Теперь одношаговое матричное умножение имеет 1 преобразователь и 1 редуктор. Формула:

Mapper for Matrix A (k, v)=((i, k), (A, j, Aij)) for all k
Mapper for Matrix B (k, v)=((i, k), (B, j, Bjk)) for all i

Поэтому вычисление картографа для Матрицы A:

# k, i, j computes the number of times it occurs.
# Here all are 2, therefore when k=1, i can have 
# 2 values 1 & 2, each case can have 2 further
# values of j=1 and j=2. Substituting all values 
# in formula

k=1  i=1  j=1   ((1, 1), (A, 1, 1)) 
          j=2   ((1, 1), (A, 2, 2))   
     i=2  j=1   ((2, 1), (A, 1, 3))
          j=2   ((2, 1), (A, 2, 4)) 

k=2  i=1  j=1   ((1, 2), (A, 1, 1))
          j=2   ((1, 2), (A, 2, 2))   
     i=2  j=1   ((2, 2), (A, 1, 3))
          j=2   ((2, 2), (A, 2, 4))

Вычисление картографа для Матрицы B

 i = 1 j = 1 k = 1 ((1, 1), (B, 1, 5)) 
          k = 2 ((1, 2), (B, 1, 6))   
     j = 2 k = 1 ((1, 1), (B, 2, 7))
          j = 2 ((1, 2), (B, 2, 8)) 

i = 2 j = 1 k = 1 ((2, 1), (B, 1, 5))
          к = 2 ((2, 2), (В, 1, 6))   
     j = 2 k = 1 ((2, 1), (B, 2, 7))
          к = 2 ((2, 2), (В, 2, 8))

Формула Reducer:

Reducer(k, v)=(i, k)=>Make sorted Alist and Blist
(i, k) => Summation (Aij * Bjk)) for j
Output =>((i, k), sum)

Поэтому вычисление редуктора:

 # Мы можем наблюдать из вычислений Mapper 
# что 4 пары являются общими (1, 1), (1, 2),
# (2, 1) и (2, 2)
# Сделайте отдельный список для Matrix A & 
# B с соседними значениями, взятыми из 
# Шаг Mapper выше:

(1, 1) => Alist = {(A, 1, 1), (A, 2, 2)}
        Блист = {(B, 1, 5), (B, 2, 7)}
        Теперь Aij x Bjk: [(1 * 5) + (2 * 7)] = 19 ------- (i)

(1, 2) => Alist = {(A, 1, 1), (A, 2, 2)}
        Блист = {(B, 1, 6), (B, 2, 8)}
        Теперь Aij x Bjk: [(1 * 6) + (2 * 8)] = 22 ------- (ii)

(2, 1) => Alist = {(A, 1, 3), (A, 2, 4)}
        Блист = {(B, 1, 5), (B, 2, 7)}
        Теперь Aij x Bjk: [(3 * 5) + (4 * 7)] = 43 ------- (iii)

(2, 2) => Alist = {(A, 1, 3), (A, 2, 4)}
        Блист = {(B, 1, 6), (B, 2, 8)}
        Теперь Aij x Bjk: [(3 * 6) + (4 * 8)] = 50 ------- (iv)

Из (i), (ii), (iii) и (iv) заключаем, что
((1, 1), 19)
((1, 2), 22)
((2, 1), 43)
((2, 2), 50)

Таким образом, окончательная матрица:

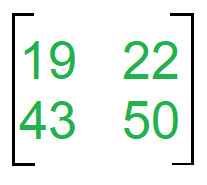
Окончательный результат умножения матрицы.

Hadoop

Умножение матриц с 1 шагом MapReduce

РЕКОМЕНДУЕМЫЕ СТАТЬИ