Удаление в дереве AVL
Мы обсудили вставку AVL в предыдущем посте. В этом посте мы будем следовать аналогичному подходу к удалению.
Шаги для удаления .
Чтобы убедиться, что данное дерево остается AVL после каждого удаления, мы должны дополнить стандартную операцию удаления BST, чтобы выполнить некоторую повторную балансировку. Ниже приведены две основные операции, которые можно выполнить для перебалансировки BST без нарушения свойства BST (клавиши (слева) < клавиша (корень) < клавиши (справа)).
- Левое вращение
- Правое вращение
T1, T2 and T3 are subtrees of the tree rooted with y (on left side)
or x (on right side)
y x
/ Right Rotation /
x T3 – - – - – - – > T1 y
/ < - - - - - - - /
T1 T2 Left Rotation T2 T3
Keys in both of the above trees follow the following order
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.Пусть w будет удаляемым узлом
- Выполните стандартное удаление BST для w.
- Начиная с w, идите вверх и найдите первый несбалансированный узел. Пусть z будет первым несбалансированным узлом, y будет дочерним элементом z большей высоты, а x будет дочерним элементом большей высоты y. Обратите внимание, что определения x и y отличаются от вставки здесь.
- Перебалансируйте дерево, выполнив соответствующие повороты поддерева с корнем z. Может быть 4 возможных случая, которые необходимо обработать, поскольку x, y и z могут быть расположены 4 способами. Ниже приведены возможные 4 схемы:
- y — левый дочерний элемент z, а x — левый дочерний элемент y (левый левый регистр)
- y — левый дочерний элемент z, а x — правый дочерний элемент y (лево-правый случай)
- y является правым дочерним элементом z, а x является правым дочерним элементом y (правильный правильный случай)
- y — правый дочерний элемент z, а x — левый дочерний элемент y (правый левый случай)
Как и вставка, ниже приведены операции, которые необходимо выполнить в вышеупомянутых 4 случаях. Обратите внимание, что, в отличие от вставки, исправление узла z не исправит все дерево AVL. После исправления z нам, возможно, придется также исправить предков z (доказательство см. в этой видео-лекции)
а) Левый левый корпус
T1, T2, T3 and T4 are subtrees.
z y
/ /
y T4 Right Rotate (z) x z
/ - - - - - - - - -> / /
x T3 T1 T2 T3 T4
/
T1 T2б) левый правый корпус
z z x
/ / /
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ - - - - - - - - -> / - - - - - - - -> / /
T1 x y T3 T1 T2 T3 T4
/ /
T2 T3 T1 T2c) Правильный случай
z y
/ /
T1 y Left Rotate(z) z x
/ - - - - - - - -> / /
T2 x T1 T2 T3 T4
/
T3 T4г) Правый левый случай
z z x
/ / /
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ - - - - - - - - -> / - - - - - - - -> / /
x T4 T2 y T1 T2 T3 T4
/ /
T2 T3 T3 T4В отличие от вставки, при удалении после поворота в точке z нам, возможно, придется выполнить поворот в предках z. Таким образом, мы должны продолжать отслеживать путь, пока не достигнем корня.
Пример:
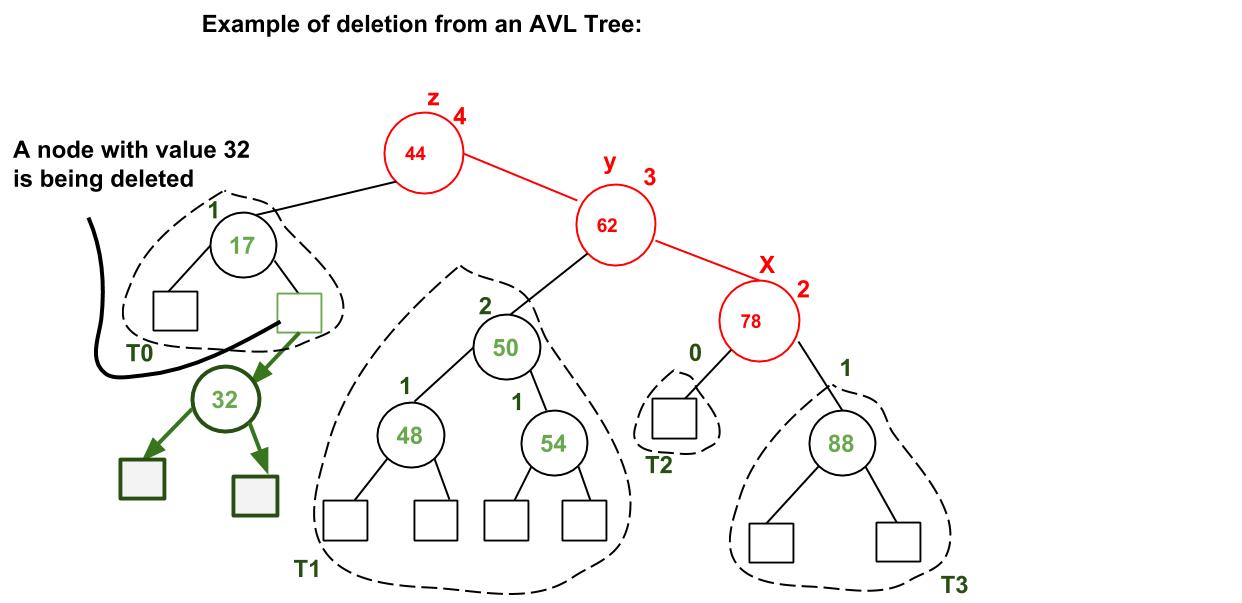
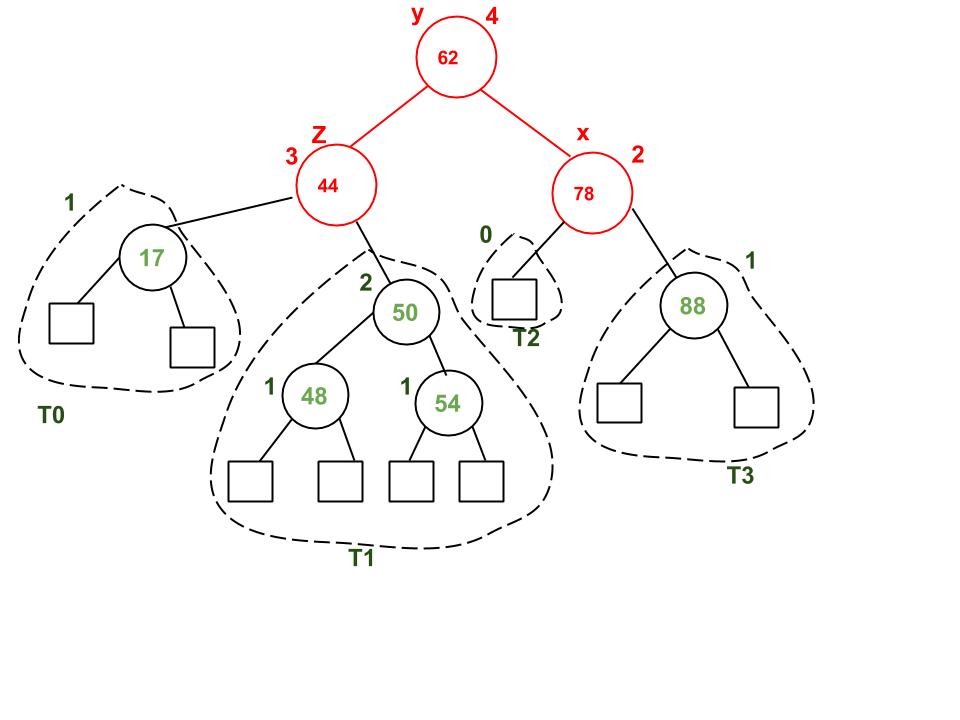
Узел со значением 32 удаляется. После удаления 32 мы перемещаемся вверх и находим первый несбалансированный узел, который равен 44. Мы помечаем его как z, его более высокий дочерний элемент как y, который равен 62, и более высокий дочерний элемент y как x, который может быть либо 78, либо 50, поскольку оба одинаковой высоты. Мы рассмотрели 78. Теперь случай Right Right, поэтому мы выполняем левое вращение.
C реализация
Ниже приведена реализация C для удаления дерева AVL. Следующая реализация C использует рекурсивное удаление BST в качестве основы. При рекурсивном удалении BST после удаления мы получаем указатели на всех предков один за другим снизу вверх. Поэтому нам не нужен родительский указатель для перемещения вверх. Сам рекурсивный код перемещается вверх и посещает всех предков удаленного узла.
- Выполните обычное удаление BST.
- Текущий узел должен быть одним из предков удаленного узла. Обновите высоту текущего узла.
- Получите коэффициент баланса (высота левого поддерева — высота правого поддерева) текущего узла.
- Если коэффициент баланса больше 1, то текущий узел несбалансирован, и мы находимся либо в случае лево-лево, либо в случае лево-право. Чтобы проверить, является ли это случаем Left Left или Left Right, получите коэффициент баланса левого поддерева. Если коэффициент баланса левого поддерева больше или равен 0, то это левый левый случай, иначе левый правый случай.
- Если коэффициент баланса меньше -1, то текущий узел несбалансирован, и мы находимся либо в случае Right Right, либо в случае Right Left. Чтобы проверить, является ли это случаем Right Right или Right Left, получите коэффициент баланса правого поддерева. Если коэффициент баланса правого поддерева меньше или равен 0, то это правый правый случай, иначе правый левый случай.
Выход:
Preorder traversal of the constructed AVL tree is 9 1 0 -1 5 2 6 10 11 Preorder traversal after deletion of 10 1 0 -1 9 5 2 6 11
Сложность времени: операции поворота (левый и правый поворот) занимают постоянное время, так как там изменяется только несколько указателей. Обновление высоты и получение коэффициента баланса также занимают постоянное время. Таким образом, временная сложность удаления AVL остается такой же, как удаление BST, которое составляет O (h), где h - высота дерева. Поскольку дерево AVL сбалансировано, высота равна O (Logn). Таким образом, временная сложность удаления AVL составляет O (Log n).
Преимущества деревьев АВЛ
- Он всегда сбалансирован по высоте
- Высота никогда не выходит за пределы LogN, где N — количество узлов.
- Это дает лучший поиск, чем по сравнению с двоичным деревом поиска.
- Он имеет возможности самобалансировки
Сводка деревьев AVL
- Это самобалансирующиеся бинарные деревья поиска.
- Коэффициент балансировки находится в диапазоне -1, 0 и +1.
- Когда коэффициент балансировки выходит за пределы диапазона, необходимо выполнить вращения
- Время вставки, удаления и поиска равно O(log N).
- Дерево AVL в основном используется там, где поиск выполняется чаще, чем операции вставки и удаления.