Типы функций активации в ИНС

Биологическая нейронная сеть была смоделирована в виде искусственных нейронных сетей. с искусственными нейронами, имитирующими функцию биологического нейрона. Искусственный нейрон изображен на картинке ниже:

Структура искусственного нейрона

Каждый нейрон состоит из трех основных компонентов:

1. Набор i-синапсов, имеющих вес w _i . Сигнал x _i формирует вход в i-й синапс, имеющий вес w _i . Значение любого веса может быть положительным или отрицательным. Положительный вес имеет необычайный эффект, в то время как отрицательный вес оказывает тормозящее влияние на выходной сигнал суммирующего соединения.
2. Суммирующий переход для входных сигналов взвешивается соответствующим синаптическим весом. Поскольку это линейный сумматор или сумматор взвешенных входных сигналов, выходной сигнал соединения суммирования может быть выражен следующим образом:
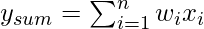
3. Функция активации порога (или просто функция активации, также известная как функция сжатия ) приводит к выходному сигналу только тогда, когда входной сигнал, превышающий определенное пороговое значение, поступает как вход. По поведению он похож на биологический нейрон, который передает сигнал только тогда, когда общий входной сигнал достигает порога срабатывания.

Типы функции активации:

Существуют разные типы функций активации. Наиболее часто используемые функции активации перечислены ниже:

A. Функция идентификации: функция идентификации используется как функция активации для входного уровня. Это линейная функция, имеющая вид

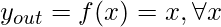
Очевидно, что вывод остается таким же, как и ввод.

B. Пороговая / ступенчатая функция: это часто используемая функция активации. Как показано на диаграмме, он дает 1, так как выход на входе либо 0, либо положительный. Если вход отрицательный, на выходе будет 0 . Выражая это математически,

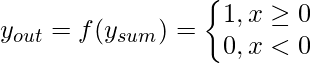
Пороговая функция почти аналогична ступенчатой, с той лишь разницей, что 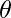используется как пороговое значение вместо. Выражаясь математически,

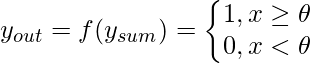
C. Функция ReLU (Rectified Linear Unit): это наиболее часто используемая функция активации в области сверточных нейронных сетей и глубокого обучения. Он имеет вид:

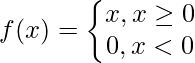
Это означает, что f (x) равно нулю, когда x меньше нуля, и f (x) равно x, когда x больше или равно нулю. Эта функция дифференцируема , за исключением единственной точки x = 0. В этом смысле производная ReLU на самом деле является дочерней производной.

D. Сигмовидная функция: это наиболее часто используемая функция активации в нейронных сетях. Потребность в сигмовидной функции проистекает из того факта, что многие алгоритмы обучения требуют, чтобы функция активации была дифференцируемой и, следовательно, непрерывной. Есть два типа сигмовидной функции:

1. Двоичная сигмовидная функция.

Бинарная сигмовидная функция имеет вид: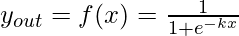

, где k = крутизна или параметр наклона. Варьируя значение k, можно получить сигмовидную функцию с разными наклонами. Он имеет диапазон (0,1). Наклон начала координат k / 4. Когда значение k становится очень большим, сигмовидная функция становится пороговой.

2. Биполярная сигмовидная функция.

Биполярная сигмовидная функция имеет вид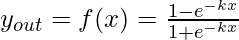

Диапазон значений сигмовидной функции может варьироваться в зависимости от приложения. Однако чаще всего используется диапазон (-1, + 1).

E. Гиперболическая касательная функция: она биполярная по своей природе. Это широко используемая функция активации для особого типа нейронной сети, известной как сеть обратного распространения. Функция гиперболического тангенса имеет вид

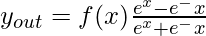
Эта функция аналогична биполярной сигмовидной функции.