Преобразование регулярного выражения в конечные автоматы

Поскольку регулярные выражения могут быть построены из конечных автоматов с использованием метода исключения состояний, обратный метод, метод декомпозиции состояний, может использоваться для построения конечных автоматов из заданных регулярных выражений.

Примечание. Этот метод создаст NFA (с ε-переходами или без них, в зависимости от выражения) для заданного регулярного выражения, которое может быть преобразовано в DFA с помощью преобразования NFA в DFA.

Метод декомпозиции состояния

Теорема: каждый язык, определяемый регулярным выражением, также определяется конечными автоматами.

Доказательство. Предположим, что L = L(R) для регулярного выражения R. Мы докажем, что L = L(M) для некоторого ε-НКА M с:

1) Ровно одно принимающее состояние.

2) Нет входящих ребер в начальном состоянии.

3) Нет исходящих ребер в принимающем состоянии.

Доказательство проводится структурной индукцией по R, выполнив следующие шаги:

Шаг 1: Создайте начальное состояние, скажем, q ₁ , и конечное состояние, скажем, q ₂ . Обозначьте переход от q ₁ к q ₂ как заданное регулярное выражение R, как на рис. 1. Но если R равно (Q) ^* , замыканию Клини другого регулярного выражения Q, тогда создайте одно начальное состояние, которое также будет конечное состояние, как на рис. 2.

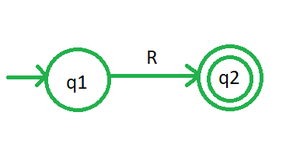
Рисунок 1

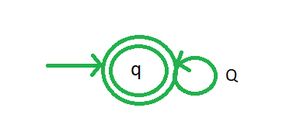
Рис 2

Шаг 2: Повторяйте следующие правила (метод декомпозиции состояния), рассматривая сначала оператор регулярного выражения с наименьшим приоритетом, пока в выражении не останется ни одного оператора. Приоритет операторов в регулярных выражениях определяется как Union < Concatenation < Kleene Closure.

Оператор объединения (+) можно исключить, введя параллельные ребра между двумя состояниями следующим образом.

Оператор конкатенации («.» или вообще без оператора ) можно исключить, введя новое состояние между состояниями следующим образом.

Замыкание Клини (*) может быть устранено путем введения циклов в состояниях на основе следующих условий:

1. Если имеется только одно исходящее ребро в крайнем левом состоянии, т. е. A в переходе A -> B, то ввести петлю в состоянии A и обозначить ребро A в B как ε-переход, как показано на рис. 5.

2. В противном случае, если имеется только одно входящее ребро в крайнем правом состоянии, т. е. B в переходе A -> B, то введите петлю в состоянии B и пометьте ребро A в B как ε-переход, как показано на рис. Рис 6.

3. В противном случае введите новое состояние между двумя состояниями, имеющими петлю, помеченную как выражение. Новое состояние будет иметь ε-переходы с предыдущими состояниями следующим образом, как показано на рис. 7.

Пример:

Постройте конечные автоматы для регулярного выражения, R = (ab + ba) ^*

Решение:

Шаг 1: Поскольку данное выражение R имеет форму (Q) ^* , поэтому мы создадим одно начальное состояние, которое также будет конечным состоянием, с петлей, помеченной (ab + ba), как показано на рис. 8. (См. рис. 2 выше)

Шаг 2:

A. В качестве оператора наименьшего приоритета в выражении используется объединение (+). Поэтому мы введем параллельные ребра (здесь параллельные петли) для «ab» и «ba», как показано на рис. 9.

B. Теперь у нас есть две метки с операторами конкатенации (ни один оператор, упомянутый между двумя переменными, не является конкатенацией), поэтому мы удаляем их одну за другой, вводя новые состояния, q ₁ и q ₂ , как показано на рис. 10 и рис. 11. (см. рис. 4 выше)

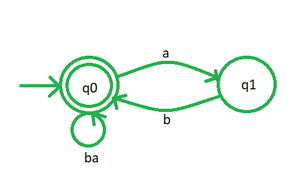
Рис. 10

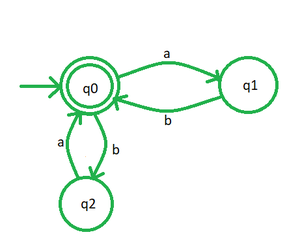
Рис. 11

Шаг 3: Поскольку операторов не осталось, мы можем сказать, что рис. 11 — это искомый конечный автомат (НКА).