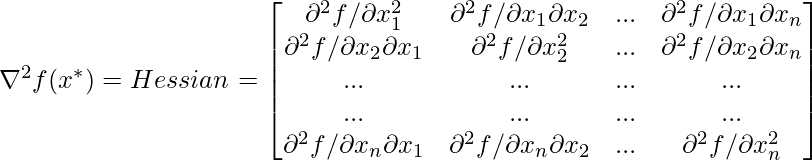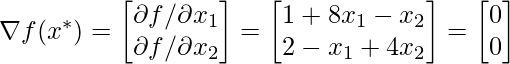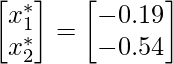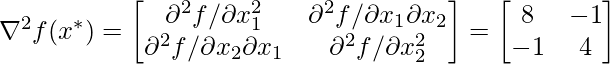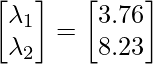Неограниченная многомерная оптимизация
Википедия определяет оптимизацию как проблему, при которой вы максимизируете или минимизируете реальную функцию, систематически выбирая входные значения из разрешенного набора и вычисляя значение функции. Это означает, что когда мы говорим об оптимизации, мы всегда заинтересованы в поиске лучшего решения. Итак, предположим, что у человека есть некоторая функциональная форма (например, в форме f (x)), и он пытается найти лучшее решение для этой функциональной формы. Что значит лучше всего? Можно сказать, что он заинтересован в минимизации этой функциональной формы или в максимизации этой функциональной формы.
Как правило, задача оптимизации состоит из трех компонентов.
минимизировать f (x),
по x,
при условии a <x <b
где, f (x): целевая функция
x: переменная решения
a <x <b: ограничение
Что такое многомерная задача оптимизации?
В задаче многомерной оптимизации есть несколько переменных, которые действуют как переменные решения в задаче оптимизации.
z = f (x 1 , x 2 , x 3 … ..x n )
Итак, когда вы смотрите на эти типы проблем, общая функция z может быть некоторой нелинейной функцией переменных решения от x 1 , x 2 , x 3 до x n . Итак, есть n переменных, которыми можно манипулировать или выбирать для оптимизации этой функции z. Обратите внимание, что можно объяснить одномерную оптимизацию, используя изображения в двух измерениях, потому что в направлении x у нас было значение переменной решения, а в направлении y - значение функции. Однако, если это многомерная оптимизация, тогда мы должны использовать изображения в трех измерениях, и если переменные решения больше 2, тогда это трудно визуализировать.
Что такое неограниченная многомерная оптимизация?
Судя по названию, многомерная оптимизация без ограничений называется неограниченной многомерной оптимизацией.
Пример :
мин f (x)
по x̄
x̄ ∈ R n
Итак, когда вы смотрите на эту проблему оптимизации, вы обычно пишете ее в приведенной выше форме, где вы говорите, что собираетесь минимизировать f (x), и эта функция называется целевой функцией. И переменная, которую вы можете использовать для минимизации этой функции, которая называется переменной решения, написана ниже, например, здесь относительно x; и вы также говорите, что x является непрерывным, то есть он может принимать любое значение в строке действительных чисел.
Необходимые и достаточные условия того, чтобы x̄ * был минимизатором функции f (x̄ * )
In case of multivariate optimization the necessary and sufficient conditions for x̄* to be the minimizer of the function f(x̄) are:
First-order necessary condition: ∇ f(x̄*) = 0
Second-order sufficiency condition: ∇ 2 f(x̄*) has to be positive definite.
where,
,and
Давайте быстро решим численный пример, чтобы лучше понять эти условия.
Числовой пример
Проблема: минРешение: По условию первого порядка
Решая два уравнения, мы получили значение а также
в виде
Чтобы проверить, является ли это точкой максимума или точки минимума, и для этого рассмотрим условие достаточности второго порядка. Итак, согласно условию достаточности второго порядка: И мы знаем, что матрица Гессе называется положительно определенной в точке если все собственные значения матрицы Гессе положительны. Итак, теперь давайте найдем собственные значения указанной выше матрицы Гессе. Чтобы найти собственное значение, обратитесь сюда. И чтобы найти собственное значение в python, обратитесь сюда. Таким образом, собственное значение указанной выше матрицы гессиана равно Таким образом, оба собственных значения оказались положительными; это означает, что это точка минимума.