Многомерная оптимизация - условия KKT

Что такое многомерная задача оптимизации?

В задаче многомерной оптимизации есть несколько переменных, которые действуют как переменные решения в задаче оптимизации.

z = f (x ₁ , x ₂ , x ₃ … ..x _n )

Итак, когда вы смотрите на эти типы проблем, общая функция z может быть некоторой нелинейной функцией переменных решения от x ₁ , x ₂ , x ₃ до x _n . Итак, есть n переменных, которыми можно манипулировать или выбирать для оптимизации этой функции z. Обратите внимание, что можно объяснить одномерную оптимизацию, используя изображения в двух измерениях, потому что в направлении x у нас было значение переменной решения, а в направлении y - значение функции. Однако, если это многомерная оптимизация, тогда мы должны использовать изображения в трех измерениях, и если переменные решения больше 2, тогда это трудно визуализировать.

Почему нас интересуют Условия ККТ?

Многомерная оптимизация с ограничением неравенства : в математике неравенство - это отношение, которое выполняет неравное сравнение между двумя числами или другими математическими выражениями. Чаще всего используется для сравнения двух чисел в числовой строке по их размеру. Есть несколько различных обозначений, используемых для обозначения различных видов неравенства. Среди них <,>, ≤, ≥ - популярные обозначения для обозначения различных видов неравенств. Таким образом, если задана целевая функция с несколькими переменными решения и ограничением неравенства, то это называется так.
Пример :

мин 2x ₁ ² + 4x ₂ ²
ул
3х ₁ + 2х ₂ ≤ 12

Здесь x ₁ и x ₂ - две переменные решения с ограничением неравенством 3x ₁ + 2x ₂ ≤ 12.

Таким образом, в случае многомерной оптимизации с ограничениями-неравенствами необходимые условия для того, ^{чтобы x̄ *} был минимизирующим, - это должно выполняться Условия KKT. Так что нас интересуют условия ККТ.

Условия ККТ:

KKT расшифровывается как Karush – Kuhn – Tucker . В математической оптимизации условия Каруша – Куна – Таккера (KKT), также известные как условия Куна – Таккера , представляют собой тесты первой производной (иногда называемые необходимыми условиями первого порядка ) для того, чтобы решение в нелинейном программировании было оптимальным, при условии, что некоторые условия регулярности выполнены.

Итак, как правило, многомерные задачи оптимизации содержат ограничения как равенства, так и неравенства.

z = min f (x)
ул
h _i (x̄) = 0, i = 1, 2,… m
g _j (x̄) ≤ 0, j = 1, 2,… l

Здесь у нас есть ограничение-равенство "m" и ограничение-неравенство "l".

Вот условия для многомерных задач оптимизации с ограничениями равенства и неравенства, чтобы достичь оптимального значения.

• Условие 1 :

  
  
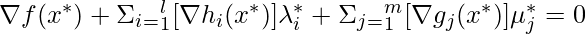  где,
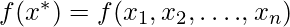   = Целевая функция
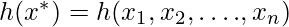   = Ограничение равенства
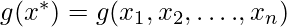   = Ограничение неравенства
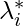   = Скалярное кратное для ограничения равенства
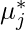   = Скалярное кратное для ограничения неравенства
  

• Условие 2 :

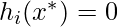   , для i = 1, ... l
  

  Это условие гарантирует, что оптимум удовлетворяет ограничениям равенства.

• Условие 3 :

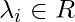   , для i = 1, ..., l
  

  Лямбда должна быть некоторым действительным числом, поэтому действительных чисел должно быть столько, сколько указано в ограничениях на равенство.

• Условие 4 :

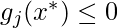   , j = 1, ..., m
  

  Как и в случае с условием 2, что оптимум удовлетворяет ограничениям равенства, нам нужно, чтобы ограничение неравенства также удовлетворялось точкой оптимума. Это гарантирует, что оптимальная точка находится в допустимой области.

• Условие 5 :

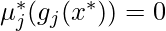
  Вот и проявляется реальная разница между условием ограничения равенства и ситуацией ограничения неравенства. И это состояние известно как условие дополнительной расслабленности. Итак, это говорит о том, что если вы возьмете произведение ограничения неравенства и соответствующего 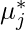тогда это должно быть 0. В основном это означает, что либо 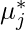равно 0, и в этом случае 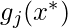может иметь любое значение, при котором выполняется это условие, или 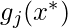равно 0, и в этом случае мы должны вычислить 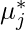и 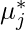которое мы вычисляем, должно быть таким, чтобы оно было положительным числом или было больше 0.

• Условие 6 :

   
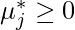   , j = 1, .., m
  

  В условии 5 мы видели, что либо 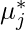равно 0, и в этом случае 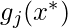может иметь любое значение, при котором выполняется это условие, или 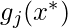равно 0, и в этом случае мы должны вычислить 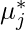и 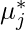которое мы вычисляем, должно быть таким, чтобы оно было положительным числом или было больше нуля. Таким образом, это условие необходимо для обеспечения того, чтобы какая бы оптимальная точка ни была у вас, не было возможности какого-либо улучшения по сравнению с оптимальной точкой. . Вот почему это условие существует.