Многомерная оптимизация - градиент и гессиан

В задаче многомерной оптимизации есть несколько переменных, которые действуют как переменные решения в задаче оптимизации.

Итак, когда вы смотрите на эти типы проблем, общая функция z может быть некоторой нелинейной функцией переменных решения от x ₁ , x ₂ , x ₃ до x _n . Итак, есть n переменных, которыми можно манипулировать или выбирать для оптимизации этой функции z. Обратите внимание, что можно объяснить одномерную оптимизацию, используя изображения в двух измерениях, потому что в направлении x у нас было значение переменной решения, а в направлении y - значение функции. Однако, если это многомерная оптимизация, тогда мы должны использовать изображения в трех измерениях, и если переменные решения больше 2, тогда это трудно визуализировать.

Градиент:
Прежде чем объяснять градиент, давайте просто сравним с необходимым условием одномерного случая. Таким образом, в случае одномерной оптимизации необходимое условие для того, чтобы x был минимизатором функции f (x):

Таким образом, производная в одномерном случае становится тем, что мы называем градиентом в многомерном случае.

В соответствии с необходимым условием первого порядка в одномерной оптимизации, например, f '(x) = 0, или его также можно записать как df / dx . Однако, поскольку существует много переменных в случае многомерного, и у нас есть много частных производных, и градиент функции f является вектором, так что в каждом компоненте можно вычислить производную функции по соответствующей переменной. Так, например, 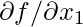это первый компонент, 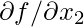второй компонент и 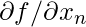это последний компонент.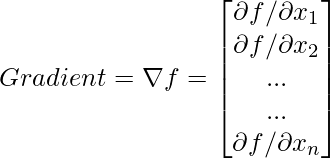

Note: Gradient of a function at a point is orthogonal to the contours.

Гессен :
Аналогично, в случае одномерной оптимизации достаточным условием для того, чтобы x был минимизатором функции f (x), является:
Условие достаточности второго порядка: f ”(x)> 0 или d ² f / dx ² > 0

И это заменяется тем, что мы называем матрицей Гессе в многомерном случае. Итак, это матрица размерности n * n, и первый компонент равен 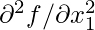, второй компонент 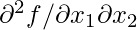и так далее.

Note:

• Hessian is a symmetric matrix.
• Hessian matrix is said to be positive definite at a point if all the eigenvalues of the Hessian matrix are positive.