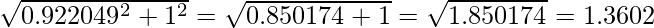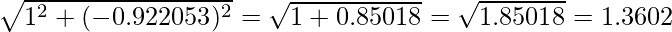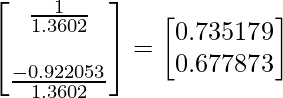Математический подход к PCA

Что такое СПС?

Основным руководящим принципом для анализа главных компонентов является ИЗВЛЕЧЕНИЕ ФУНКЦИЙ, т. Е. «Функции набора данных должны быть меньше, как и сходство друг с другом». В PCA новый набор функций извлекается из исходных функций, которые по своей природе совершенно не похожи. Таким образом, n-мерное пространство признаков преобразуется в m-мерное пространство признаков. , где размеры ортогональны друг другу.

Концепция ортогональности:

(Чтобы понять эту тему, мы должны перейти к концепции векторного пространства в линейной алгебре) Векторное пространство - это набор векторов. Их можно представить как линейную комбинацию меньшего набора векторов, называемых БАЗОВЫМИ ВЕКТОРАМИ. Таким образом, любой вектор v в векторном пространстве можно представить как:

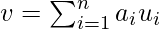
где a представляет n скаляров, а u представляет базисные векторы. Базисные векторы ортогональны друг другу. Ортогональность векторов можно представить как расширение перпендикулярных векторов в двумерном векторном пространстве . Таким образом, наш вектор признаков (набор данных) может быть преобразован в набор основных компонентов (как и базисные векторы).

Задачи PCA:

1. Новые функции отличаются, т.е. ковариация между новыми функциями (в случае PCA, они являются главными компонентами) равна 0 .
2. Основные компоненты генерируются в порядке изменчивости собираемых данных. Следовательно, первый главный компонент должен отражать максимальную изменчивость, второй - следующую по величине изменчивость и т. Д.
3. Сумма дисперсии новых функций / основных компонентов должна быть равна сумме дисперсии исходных функций.

Работа PCA:

PCA работает над процессом, называемым разложением по собственным значениям ковариационной матрицы набора данных. Шаги следующие:

• Сначала вычислите ковариационную матрицу набора данных.
• Затем вычислите собственные векторы ковариационной матрицы.
• Собственный вектор, имеющий наивысшее собственное значение, представляет направление, в котором существует наибольшая дисперсия. Так что это поможет определить первый главный компонент.
• Собственный вектор, имеющий следующее наивысшее собственное значение, представляет направление, в котором данные имеют наибольшую оставшуюся дисперсию, а также ортогонален первому направлению. Таким образом, это помогает идентифицировать второй главный компонент.
• Как это, определить верхние "k" собственных векторов, имеющих верхние "k" собственных значений, чтобы получить "k" главных компонентов.

Числовой для PCA:

Рассмотрим следующий набор данных

Шаг 1. Стандартизация набора данных

Означает для = 1,81 =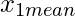

Означает для = 1,91 =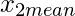

Мы изменим набор данных.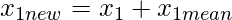

	0,69	-1,31	0,39	0,09	1,29	0,49	0,19	-0,81	-0,31	-0,71
	0,49	-1,21	0,99	0,29	1.09	0,79	-0,31	-0,81	-0,31	-1.01

Шаг 2: Найдите собственные значения и собственные векторы

Матрица корреляции c =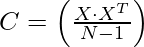

где X - матрица набора данных (в данном числовом выражении это матрица 10 X 2).

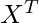- это транспонирование X (в данном числовом выражении это матрица 2 X 10), а N - количество элементов = 10

Так,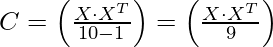

{Итак, чтобы вычислить матрицу корреляции, мы должны произвести умножение матрицы набора данных на ее транспонирование}

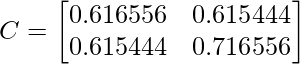
Используя уравнение, | С - 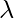Я | = 0 - уравнение (i), где { lambda - собственное значение, а I - матрица идентичности}

Итак, решая уравнение (i)

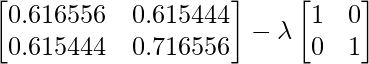
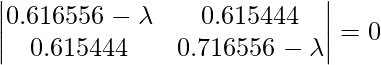
Взяв определитель левой части, получим

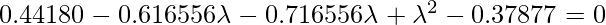
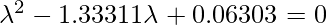
Получаем два значения для 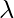, то есть ( 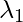) = 1,28403 и ( ) = 0,0490834 . Теперь нам нужно найти собственные векторы для собственных значений 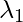а также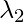

Чтобы найти собственные векторы из собственных значений, мы будем использовать следующий подход:

Сначала мы найдем собственные векторы для собственного значения 1,28403, используя уравнение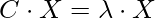

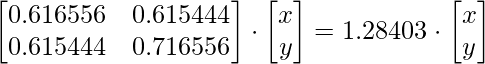
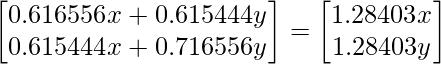
Решая матрицы, получаем

0,616556x + 0,615444y = 1,28403x; x = 0,922049 и

(x и y принадлежат матрице X), поэтому, если мы положим y = 1, x окажется равным 0,922049. Итак, теперь обновленная матрица X будет выглядеть так:

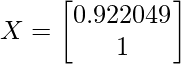
IMP: Till now we haven’t reached to the eigenvectors, we have to a bit of modifications in the X matrix. They are as follows:

A. Find the square root of the sum of the squares of the element in X matrix i.e.

B. Now divide the elements of the X matrix by the number 1.3602 (just found that)

 

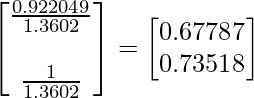
So now we found the eigenvectors for the eigenvector , they are 0.67787 and 0.73518

Во-вторых, мы найдем собственные векторы для собственного значения 0,0490834, используя уравнение {тот же подход, что и на предыдущем шаге)

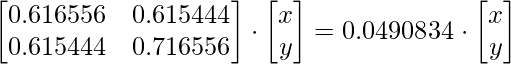
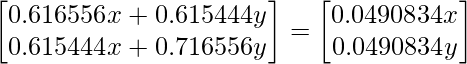
Решая натрисы, получаем

0,616556x + 0,615444y = 0,0490834x; у = -0,922053

(x и y принадлежат матрице X), поэтому, если мы положим x = 1, y будет равно -0,922053 Итак, теперь обновленная матрица X будет выглядеть так:

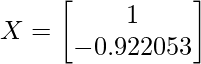
IMP: Till now we haven’t reached to the eigenvectors, we have to a bit of modifications in the X matrix. They are as follows:

A. Find the square root of the sum of the squares of the elemnts in X matrix i.e.

B. Now divide the elements of the X matrix by the number 1.3602 (just found that)

So now we found the eigenvectors for the eigenvector lambda_2, they are 0.735176 and 0.677873

Сумма собственных значений ( 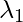) а также ( ) = 1,28403 + 0,0490834 = 1,33 = Общая дисперсия {Большая часть дисперсии происходит от }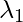

Шаг 3: расположите собственные значения

Собственный вектор с наивысшим собственным значением - это главный компонент набора данных. Итак, в этом случае собственные векторы лямбда1 являются главными компонентами.

{В основном, чтобы завершить численное, нам нужно решить только до этого шага, но если нам нужно доказать, почему мы выбрали именно этот собственный вектор, мы должны выполнить шаги с 4 по 6 }

Шаг 4: сформируйте вектор признаков

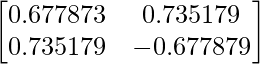Это ВЕКТОР ОСОБЕННОСТИ для числового

Где первый столбец - собственные векторы 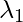& второй столбец - собственные векторы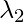

Шаг 5: преобразовать исходный набор данных

Используйте уравнение Z = XV

Шаг 6: восстановление данных

Используйте уравнение X = 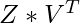( является транспонированием V), X = данные строки с нулевым средним

Итак, чтобы восстановить исходные данные, мы следуем:

Исходный набор данных строки = нулевое среднее значение строки + исходное среднее значение

Таким образом, для собственных векторов первого собственного значения данные могут быть восстановлены аналогично исходному набору данных. Таким образом, мы можем сказать, что основным компонентом набора данных является 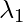равно 1,28403, за которым следует то есть 0,0490834