Локальный и глобальный оптимумы в универсальной оптимизации
Одновременная оптимизация - это простой случай задачи нелинейной оптимизации с неограниченным случаем, когда нет ограничений. Универсальная оптимизация может быть определена как нелинейная оптимизация без ограничений, и в этой оптимизации есть только одна переменная решения, для которой мы пытаемся найти значение.
min f(x) such that x ∈ R
где,
f (x) = целевая функция
x = переменная решения
Итак, когда вы смотрите на эту проблему оптимизации, вы обычно пишете ее в приведенной выше форме, где вы говорите, что собираетесь минимизировать f (x) , и эта функция называется целевой функцией. И переменная, которую вы можете использовать для минимизации этой функции, которая называется переменной решения, написана ниже, как здесь, относительно x, и вы также говорите, что x является непрерывным, то есть он может принимать любое значение в строке действительных чисел. И поскольку это задача оптимизации с одним изменением, x - это скалярная переменная, а не векторная переменная.
Выпуклая функция:
Всякий раз, когда мы говорим об одномерных задачах оптимизации, это легко визуализировать на такой двухмерной картинке.
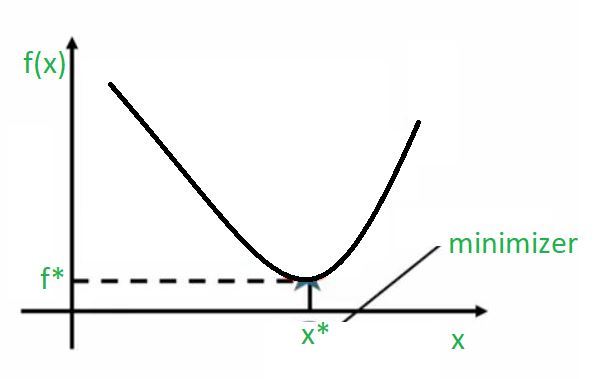
Итак, то, что у нас есть, находится на оси x, у нас есть разные значения для переменной решения x, а на оси y у нас есть значение функции. И когда вы строите это, вы можете довольно легко заметить на графике, который отмечает точку, в которой эта функция достигает своего минимального значения. Таким образом, точку, в которой эта функция достигает минимального значения, можно найти, опустив перпендикуляр на ось x. Таким образом, вы можете сказать, что x * - это фактическое значение x, при котором эта функция принимает минимальное значение, а значение, которое функция принимает в своей минимальной точке, можно определить, опустив этот перпендикуляр на ось y, и это f * является наилучшее значение, которое могла бы принять эта функция. Итак, функции этого типа называются выпуклыми функциями, потому что здесь есть только один минимум . Таким образом, нет вопроса о нескольких минимумах на выбор, здесь есть только один минимум, и он отмечен на графике. Итак, в этом случае мы бы сказали, что этот минимум является одновременно локальным и глобальным минимумом . Фактически, мы можем сказать, что это локальный минимум, потому что вблизи этой точки это лучшее решение, которое вы можете получить. И если решение, которое мы получаем в окрестности этой точки, также является лучшим решением в глобальном масштабе, мы также называем его глобальным минимумом .
Невыпуклая функция:
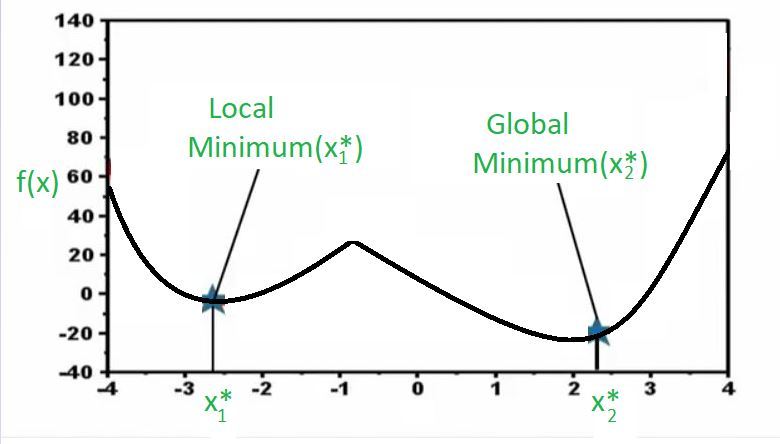
Теперь взгляните на приведенный выше график. Здесь у меня есть функция, и это снова задача одномерной оптимизации. Итак, по оси X у меня есть разные значения переменной решения, а по оси Y мы строим график функции. Теперь вы можете заметить, что есть две точки, в которых функция достигает минимума, и вы можете видеть, что когда мы говорим минимум, мы автоматически имеем в виду только локальный минимум, потому что если вы заметите эту точку x1 * на графике, в непосредственной близости от этой точки , эта функция не может иметь лучшего значения с точки зрения минимизации. Другими словами, если я нахожусь в x1 * и функция принимает это значение, если я двигаюсь вправо, значение функции будет увеличиваться, что в основном не очень хорошо для нас, потому что мы пытаемся найти минимальное значение, и если я двигаюсь слева от меня значение функции снова увеличится, что нехорошо, потому что мы находим минимум для этой функции. В основном это говорит о следующем.
Это говорит о том, что в окрестностях вы никогда не найдете места лучше, чем эта. Однако, если вы уйдете далеко, вы попадете в эту точку (x2 *), которая снова с локальной точки зрения является лучшей, потому что, если мы пойдем в правильном направлении, функция возрастет, а если мы пойдем влево, также функция увеличивается, и в этом конкретном примере также оказывается, что в целом это лучшее решение. Итак, хотя оба являются локальным минимумом в том смысле, что вблизи они являются лучшими, но этот локальный минимум (x2 *) также является глобальным минимумом, потому что, если вы возьмете весь регион, вы все равно не сможете превзойти это решение. Итак, когда у вас есть решение, которое является самым низким во всем регионе, мы называем это глобальным минимумом. И это типы функций, которые мы называем невыпуклыми функциями, в которых существует несколько локальных оптимумов, а задача оптимизатора - найти лучшее решение из множества возможных оптимальных решений.
Почему эта концепция важна для науки о данных?
Давайте установим связь между этой концепцией и наукой о данных. Эта проблема нахождения глобального минимума была реальной проблемой в нескольких алгоритмах науки о данных. Например, в 90-х годах было много ажиотажа и интереса к нейронным сетям и так далее, и в течение нескольких лет много исследований проводилось в нейронных сетях, и во многих случаях оказалось, что найти глобальное оптимальное решение было очень сложно. и во многих случаях эти нейронные сети обучены локальным оптимумам, которые недостаточно хороши для типа решаемых задач. Итак, это стало настоящей проблемой с понятием нейронных сетей, а затем в последние годы к этой проблеме вернулись, и теперь есть гораздо лучшие алгоритмы, гораздо лучшие функциональные формы и гораздо лучшие стратегии обучения. Так что вы можете достичь некоторого представления о глобальной оптимальности, и именно по этой причине у нас есть эти алгоритмы, которые возвращаются и становятся очень полезными.