Кривая B-сплайна в компьютерной графике
Предпосылка - кривая Безье
Концепция кривой B-сплайна пришла к устранению недостатков, присущих кривой Безье, поскольку все мы знаем, что обе кривые являются параметрическими по своей природе. В кривой Безье мы сталкиваемся с проблемой, когда мы меняем положение любой контрольной точки, соответствующая ей, вся форма кривой изменяется. Но здесь, в кривой B-сплайна, только определенный сегмент формы кривой изменяется или затрагивается изменением соответствующего местоположения контрольных точек.
В B-сплайновой кривой контрольные точки передают локальный контроль над формой кривой, а не глобальный контроль, как кривая Безье.
Форма кривой B-сплайна до изменения положения контрольной точки P 1 -

Форма кривой B-сплайна после изменения положения контрольной точки P 1 -

Вы можете видеть на приведенном выше рисунке, что только форма сегмента 1, поскольку мы изменили только контрольную точку P 1 , а форма сегмента 2 остается неизменной.
Кривая B-сплайна:
Как мы видим выше, кривые B-сплайнов не зависят от количества контрольных точек и состоят из плавного соединения нескольких сегментов, при этом форма каждого сегмента определяется некоторыми конкретными контрольными точками, которые находятся в этой области сегмента. Рассмотрим кривую, приведенную ниже -

Атрибуты этой кривой -
- У нас есть «n + 1» контрольных точек в приведенном выше примере, поэтому n + 1 = 8, поэтому n = 7.
- Предположим, что порядок этой кривой - «k», поэтому кривая, которую мы получим, будет иметь полиномиальную степень «k-1». Обычно говорят, что значение «k» должно быть в диапазоне: 2 ≤ k ≤ n + 1. Итак, предположим, что k = 4, поэтому степень кривой будет k-1 = 3.
- Общее количество сегментов этой кривой будет рассчитано по следующей формуле -
Всего нет. из сегментов = n - k + 2 = 7-4 + 2 = 5.
| Сегменты | Контрольные точки | Параметр |
|---|---|---|
| S 0 | P 0 , P 1 , P 2 , P 3 | 0≤t≤2 |
| S 1 | P 1 , P 2 , P 3 , P 4 | 2≤t≤3 |
| S 2 | P 2 , P 3 , P 4 , P 5 | 3≤t≤4 |
| S 3 | P 3 , P 4 , P 5 , P 6 | 4≤t≤5 |
| S 4 | P 4 , P 5 , P 6 , P 7 | 5≤t≤6 |
Узлы в кривой B-сплайна:
Точка между двумя сегментами кривой, которые соединяют друг друга с такими точками, называются узлами на кривой B-сплайна. В случае кубической полиномиальной кривой степени узлы равны «n + 4». Но в других общих случаях у нас есть «n + k + 1» узлов. Итак, для приведенной выше кривой общие векторы узлов будут -
Всего узлов = n + k + 1 = 7 + 4 + 1 = 12
Эти узловые векторы могут быть трех типов -
- Равномерное (периодическое)
- Открытая форма
- Неоднородный
Уравнение кривой B-сплайна: Уравнение кривой сплайна выглядит следующим образом:
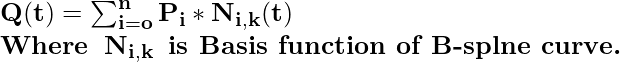
Где P i , k, t соответственно представляет контрольные точки, степень, параметр кривой.
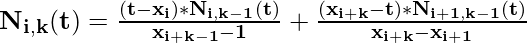
И следующие условия для x i следующие:
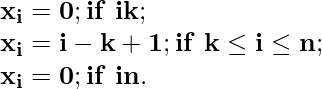
Некоторые случаи использования базовой функции:
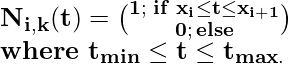
Свойства кривой B-сплайна:
- Каждая базовая функция имеет значение 0 или + для всех параметров.
- Каждая базисная функция имеет одно максимальное значение, кроме k = 1.
- Степень полинома кривой B-сплайна не зависит от количества контрольных точек, что делает его более надежным в использовании, чем кривая Безье.
- Кривая B-сплайна обеспечивает локальное управление через контрольные точки на каждом сегменте кривой.
- Сумма базисных функций для данного параметра равна единице.