Компьютерная графика - трехмерное композитное преобразование

Трехмерное преобразование - это процесс манипулирования видом трехмерного объекта относительно его исходного положения путем изменения его физических атрибутов с помощью различных методов преобразования, таких как перемещение, масштабирование, поворот, сдвиг и т. Д.

Типы трансформации:

1. Трансформация перевода
2. Масштабирование трансформации
3. Преобразование вращения
4. Трансформация сдвига
5. Преобразование отражения

Примечание: если нас просят одновременно выполнить три или более различных вида преобразований над точкой (P ₀ ), помещенной в трехмерное пространство, и предположим, что эти преобразования равны T ₁ , T ₂ и T ₃ соответственно, тогда что будем делать в таком случае?

Итак, мы увидим следующие решения

а) Очевидно, сначала последовательно применяя серию Преобразований по координатам объекта.

First we performed transformation T_1, then P_o become transformed to P_1.

Secondly, we perform transformation T₂ and the point P₁ become transformed to P_2.

Lastly, we perform transformation T₃ and we get the final result i.e; P_3,and we will get our final transformed point coordinate(P₃).

б) Второе решение, применяя преобразование Composite за один прием.

Примечание: Здесь T ₁ , T ₂ , T ₃ соответствуют их матричному условию преобразования.

Составное преобразование

Поскольку его название предполагает себя составным, здесь мы составляем два или более двух преобразований вместе и вычисляем результирующую (R) матрицу преобразования , умножая все соответствующие условия матрицы преобразования друг на друга.

Тот же эквивалентный результат, который мы получили в точке P ₀ и преобразовали ее в P ₃ в приведенном выше примере, также может быть достигнут путем прямого умножения результирующего R на точку P _0, а не выполнения преобразований T ₁ , T ₂ и T ₃ последовательно один после одного.

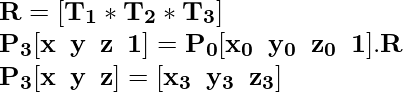
И мы получаем тот же результат, что и в нашем примере выше.

Проблема: представьте, что нам дан кубоид «OABCDEFG», над которым мы хотим выполнить

• Преобразование переноса (T ₁ ), если расстояния переноса равны D _x = 2, D _y = 3, D _z = 2, то
• Масштабирующее преобразование (T ₂ ), если масштабные коэффициенты s _x = 2, s _y = 1, s _z = 3 и напоследок выполнить,
• Трансформация сдвига (T ₃ ) в направлении x, если коэффициенты сдвига s _y = 2 и s _z = 1.

Решение: нам дан следующий кубоид

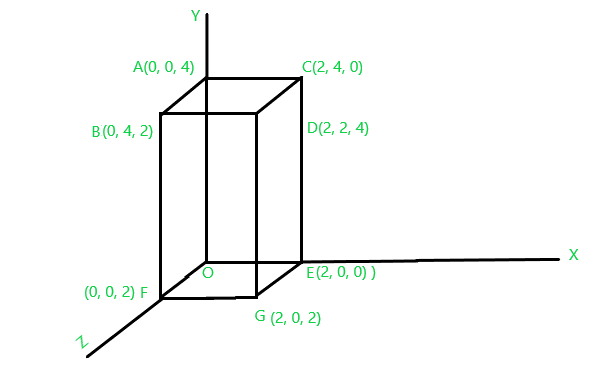
Рисунок 1

Сначала выполняем преобразование трансляции T1:

Матрица преобразования трансляции отображается как:

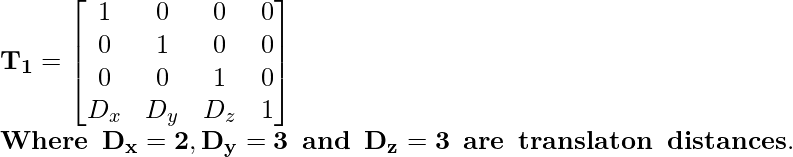[Tex] hspace {4.37cm} mathbf {T_1 = left [ begin {matrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ D_x & D_y & D_z & 1 end {matrix} right]} \ mathbf {Где hspace { 0,2 см} D_x = 2, D_y = 3 hspace {0,2 см} и hspace {0,2 см} D_z = 3 hspace {0,2 см} - это расстояние hspace {0,2 см} в трансляте hspace {0,2 см}.} [ / Tex]

Теперь примените это условие матрицы преобразования трансляции по координатам:

Для координаты O [0 0 0] вновь переведенная координата будет O ₁ :

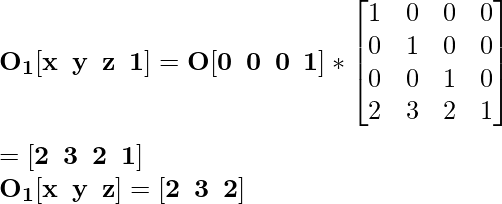
Для координаты A [0 0 4] вновь переведенная координата будет A ₁ :

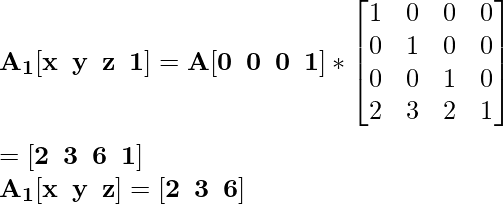
Для координаты B [0 4 2] вновь переведенная координата будет B ₁ :

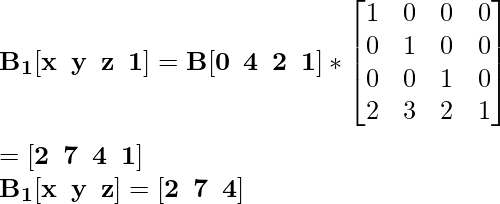
Для координаты C [2 4 0] вновь переведенная координата будет C ₁ :

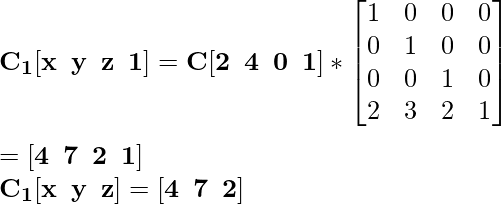
Для координаты D [2 2 4] вновь перенесенная координата будет D ₁ :

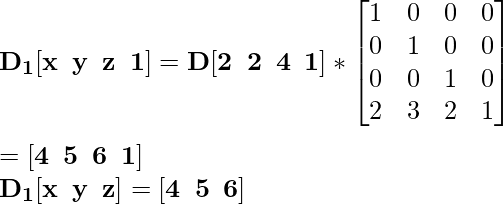
Для координаты E [2 0 0] вновь переведенная координата будет E ₁ :

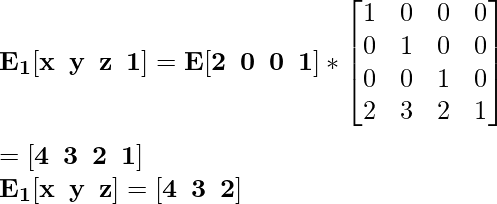
Для координаты F [0 0 2] вновь перенесенная координата будет F ₁ :

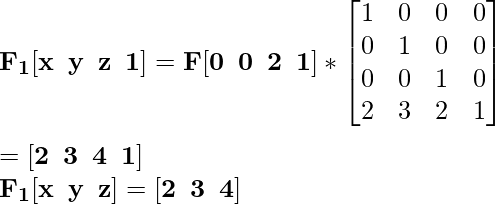
Для координаты G [2 0 2] вновь перенесенная координата будет G ₁ :

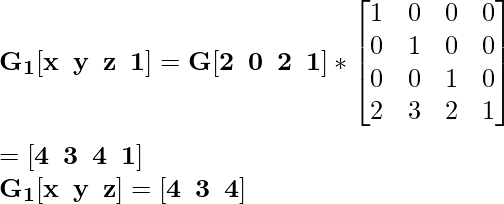
Рис.2.

Во-вторых, говорят, что мы выполняем преобразование масштабирования T ₂ :

Матрица преобразования масштабирования отображается как:

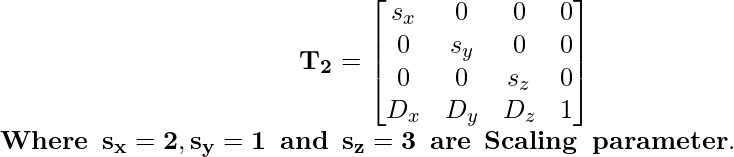
Теперь примените это условие матрицы преобразования масштабирования к координатам:

Для координаты O ₁ [2 3 2] новая масштабированная координата будет O ₂ :

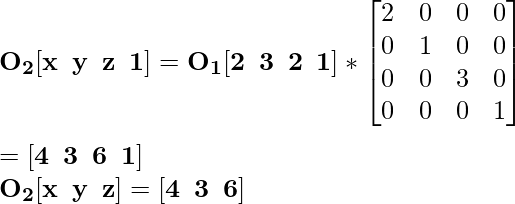
Для координаты A ₁ [2 3 6] новая масштабированная координата будет A ₂ :

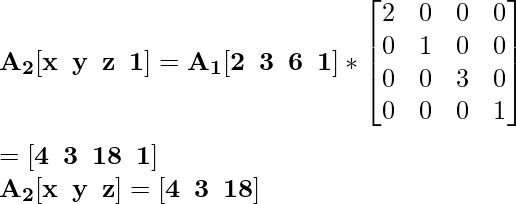
Для координаты B ₁ [2 7 4] новая масштабированная координата будет B ₂ :

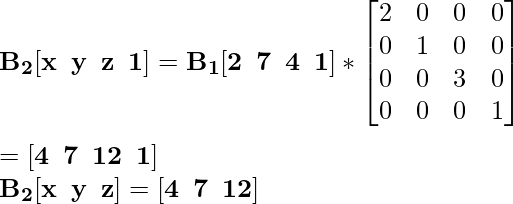
Для координаты C ₁ [4 7 2] новая масштабированная координата будет C ₂ :

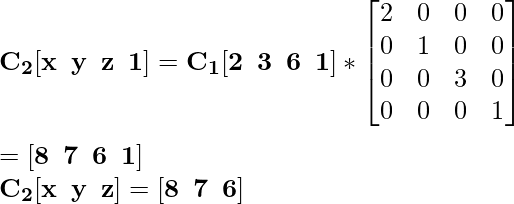
Для координаты D ₁ [4 5 6] новая масштабированная координата будет D ₂ :

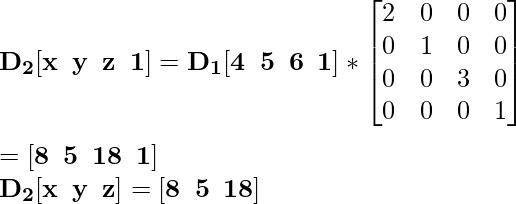
Для координаты E ₁ [4 3 2] новая масштабированная координата будет E ₂ :

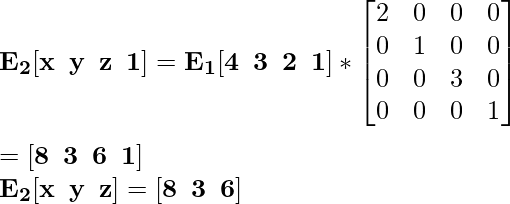
Для координаты F ₁ [2 3 4] новая масштабированная координата будет F ₂ :

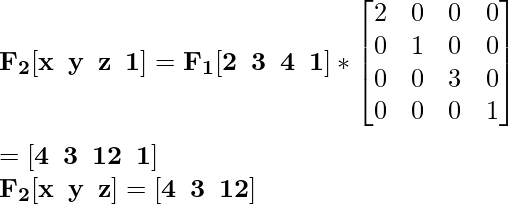
Для координаты G ₁ [4 3 4] новая масштабированная координата будет G ₂ :

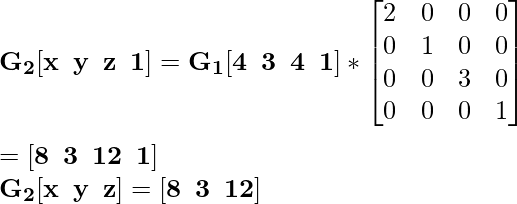
Рис.3

Наконец, мы выполняем трансформацию сдвига T ₃ в направлении оси x:

Матрица преобразования сдвига для направления x отображается как:

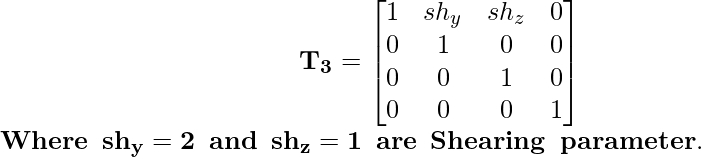
Теперь примените это условие матрицы преобразования сдвига по координатам:

Для координаты O ₂ [4 3 6] новая масштабированная координата будет O ₃ :

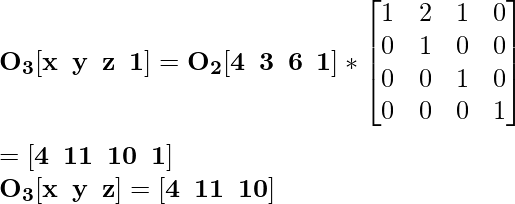
Для координаты A ₂ [4 3 18] новая масштабированная координата будет A ₃ :

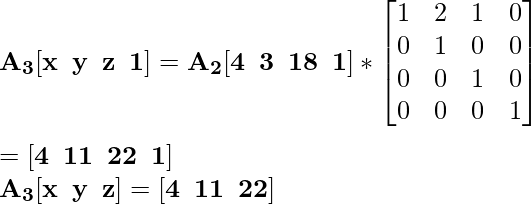
Для координаты B ₂ [4 7 12] новая масштабированная координата будет B ₃ :

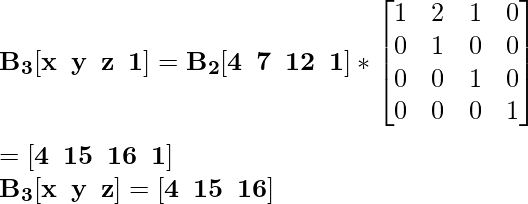
Для координаты C ₂ [8 7 6] новая масштабированная координата будет C ₃ :

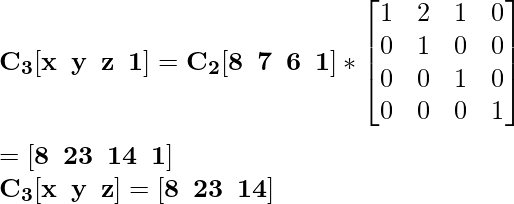
Для координаты D ₂ [8 5 18] новая масштабированная координата будет D ₃ :

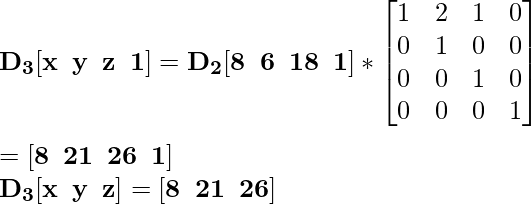
Для координаты E ₂ [8 7 6] новая масштабированная координата будет E ₃ :

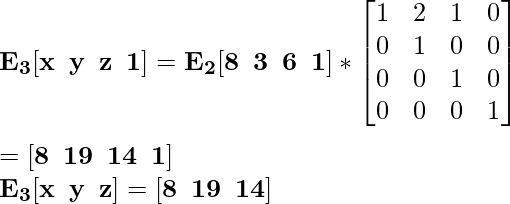
Для координаты F ₂ [4 3 12] новая масштабированная координата будет F ₃ :

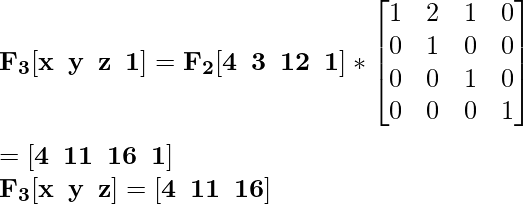
Для координаты G ₂ [8 3 12] новая масштабированная координата будет G ₃ :

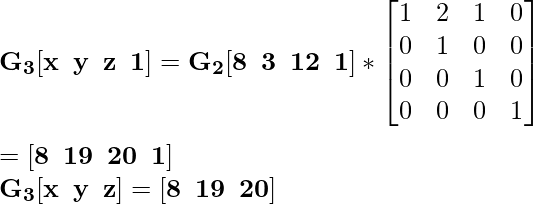
Наконец, мы получаем наш наклонный объект с измененным размером в x-направлении после выполнения преобразований T ₁ , T ₂ и T ₃ .

Рис.4

Решение через композитное преобразование

Окончательный результат, который мы получили выше для кубоида «OABCDEF», применяя преобразование T ₁ , T ₂ и T ₃ одно за другим в последовательном порядке, тот же эквивалентный результат также может быть получен с помощью концепции составного преобразования. Чтобы сначала выполнить составное преобразование, нам нужно вычислить матрицу результирующего преобразования (R) путем объединения всех выделенных представлений матрицы преобразования вместе.

Результирующая матрица преобразования будет рассчитана следующим образом:

Результирующее преобразование будет вычислено путем умножения матрицы преобразования преобразования на матрицу преобразования масштабирования, а результирующее (R ₂ ) умножение обоих будет затем умножено на последнюю заданную матрицу преобразования сдвига.

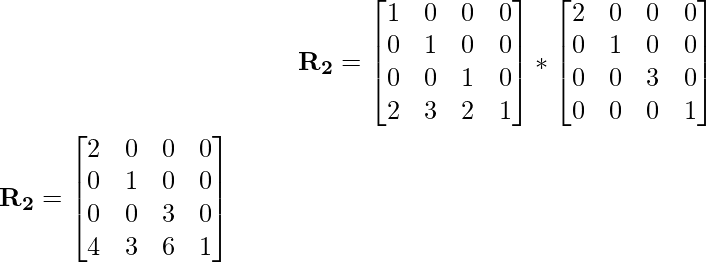
Теперь умножьте R2 на матрицу преобразования сдвига, чтобы получить результирующее R:

Теперь примените это условие матрицы преобразования к координатам:

Для координаты O [0 0 0] новая масштабированная координата будет O ₃ :

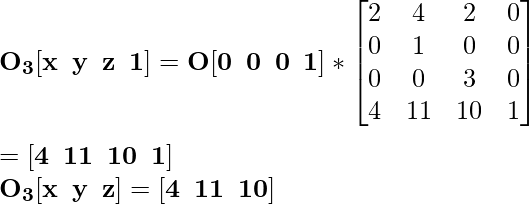
Для координаты A [0 0 4] новая масштабированная координата будет A ₃ :

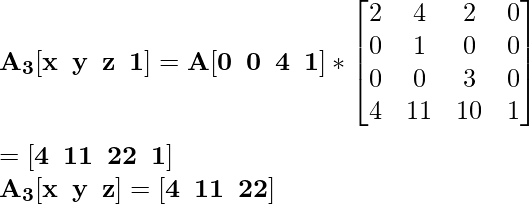
Для координаты B [0 4 2] новая масштабированная координата будет B ₃ :

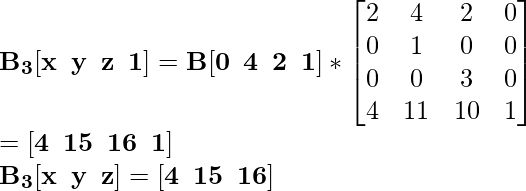
Для координаты C [2 4 0] новая масштабированная координата будет C ₃ :

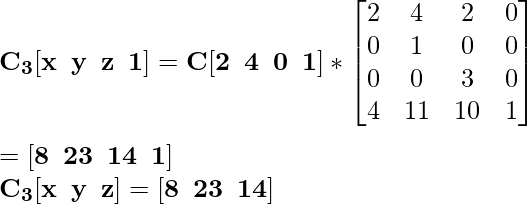
Для координаты D [2 2 4] новая масштабированная координата будет D ₃ :

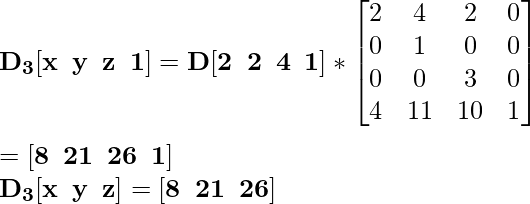
Для координаты E [2 0 0] новая масштабированная координата будет E ₃ :

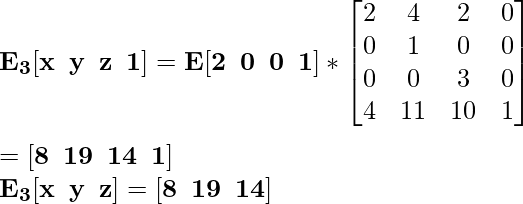
Для координаты F [0 0 2] новая масштабированная координата будет F ₃ :

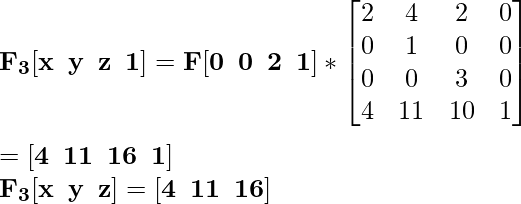
Для координаты G [2 0 2] новая масштабированная координата будет G ₃ :

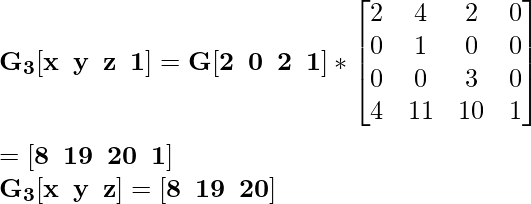
Здесь мы получаем окончательный результат за один выстрел:

Рис.5

Вниманию читателя! Не переставай учиться сейчас. Ознакомьтесь со всеми важными концепциями теории CS для собеседований по SDE с помощью курса теории CS по доступной для студентов цене и будьте готовы к работе в отрасли.