Компьютерная графика - 3D трансформация сдвига
Преобразование сдвига такое же, как и в 2D-пространстве, но здесь мы имеем дело с осями x, y и z, тогда как в 2D мы имеем дело только с осями x и y. Сдвиг - это процесс наклона объекта в трехмерном пространстве по осям x, y или z. Сдвиг изменяет (или деформирует) форму объекта. Поскольку мы обсуждаем трехмерное пространство, сдвиг также можно выполнять в любом из трех направлений, как показано ниже. Ниже приведены типы трансформации сдвига.
- Срезание по оси X.
- Стрижка в направлении y
- Срезание в направлении z.
Сдвиг в направлении X: здесь координата X остается неизменной, а координаты Y и Z изменяются. Сдвиг выполняется с помощью матрицы преобразования сдвига, которая представлена следующим образом.

Рассмотрим точку P [x, y, z] в трехмерном пространстве, над которой мы выполняем преобразование сдвига в направлении X, и она становится P '[x, y, z].
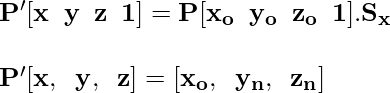
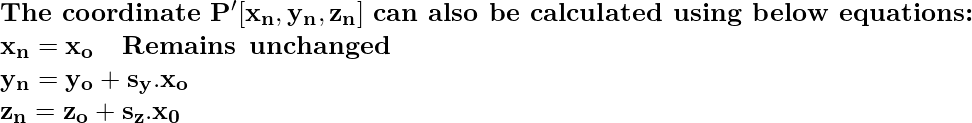
Сдвиг в направлении Y: здесь координата Y остается неизменной, а координаты X и Z изменяются. Сдвиг выполняется с помощью матрицы преобразования сдвига, которая представлена следующим образом.

Рассмотрим точку P [x, y, z] в трехмерном пространстве, над которой мы выполняем преобразование сдвига в направлении Y, и она становится P '[x, y, z].
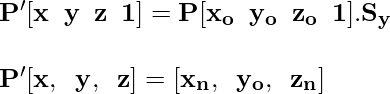
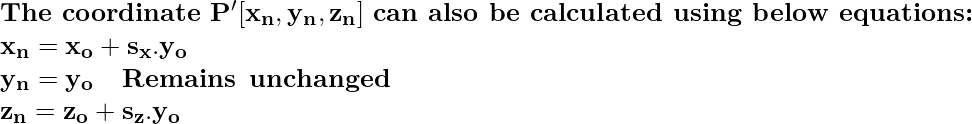
Сдвиг в направлении Z: здесь координата Z остается неизменной, в то время как координаты X и Y изменяются. Сдвиг выполняется с помощью матрицы преобразования сдвига, которая для сдвига в Z-направлении представлена следующим образом.

Рассмотрим точку P [x, y, z] в трехмерном пространстве, над которой мы выполняем преобразование сдвига в Z-направлении, и она становится P '[x, y, z].
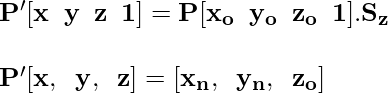
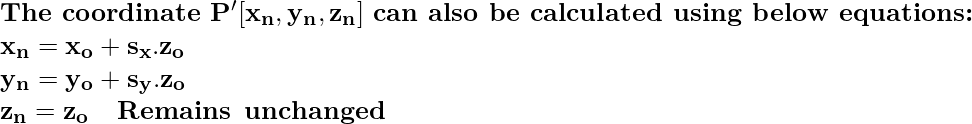
Примечание. Здесь x n , y n , z n показывают = новые значения, а x o , y o , z o показывают = старые значения.
Выполните преобразование сдвига в данном кубоиде (OABCDEFG) в направлении Z, если параметр сдвига имеет следующий вид: S x = 2, S y = 3.
Матрица преобразования сдвига для z-направления выглядит следующим образом.

И данный кубоид выглядит следующим образом:
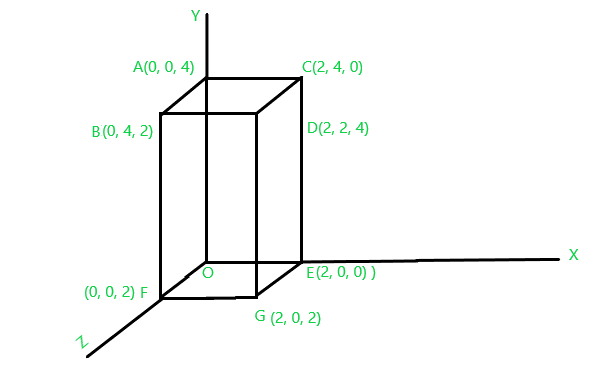
Рисунок 1
Теперь мы применим условие трансформации сдвига ко всем координатам и вычислим новые соответствующие координаты:
Точка O [0, 0, 0] становится O 'после выполнения преобразования «Отражение»:
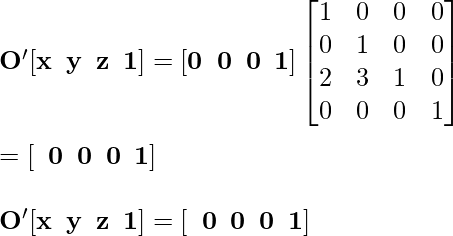
Точка A '[0, 0, 4] становится A' после выполнения преобразования Reflection:
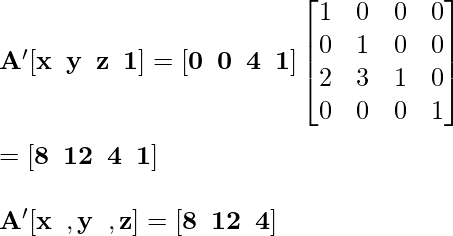
Точка B '[0, 0, 4] становится B' после выполнения преобразования «Отражение»:
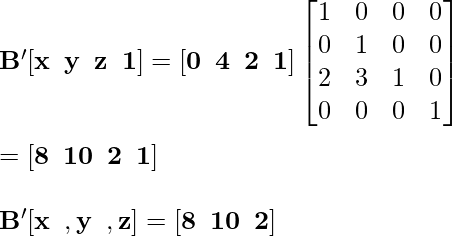
Точка C '[2, 4, 0] становится C' после выполнения преобразования Reflection:
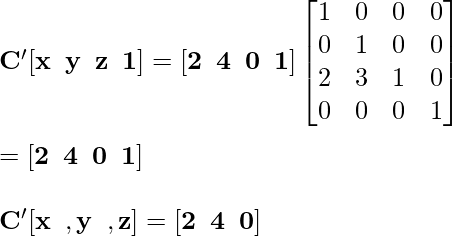
Точка D '[2, 2, 4] становится D' после выполнения преобразования «Отражение»:
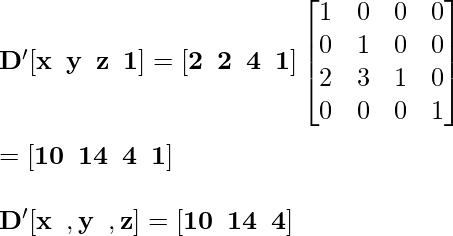
Точка E '[2, 0, 0] становится E' после выполнения преобразования Reflection:
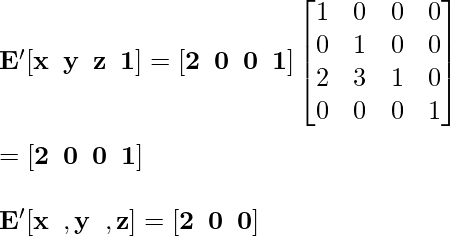
Точка F '[0, 0, 2] становится F' после выполнения преобразования «Отражение»:
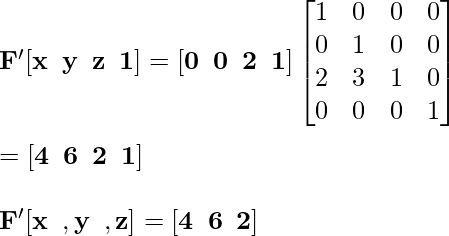
Точка G '[2, 0, 2] становится G' после выполнения преобразования «Отражение»:
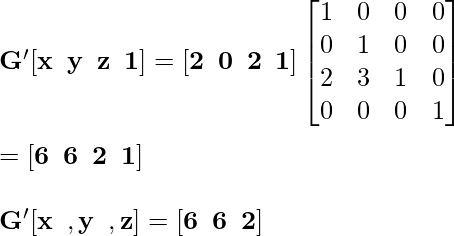
Наконец, после выполнения трансформации сдвига на данном кубоиде ваш рисунок 1 будет выглядеть, как показано ниже:
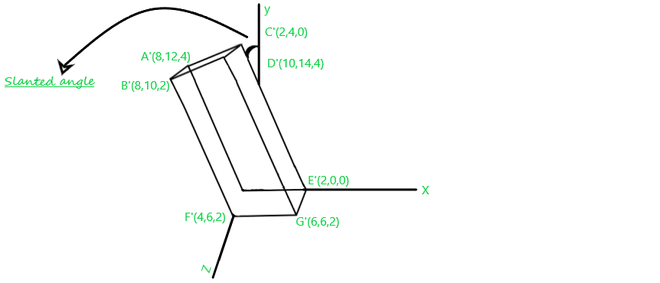
Рис.2.
Вниманию читателя! Не переставай учиться сейчас. Ознакомьтесь со всеми важными концепциями теории CS для собеседований по SDE с помощью курса теории CS по доступной для студентов цене и будьте готовы к работе в отрасли.