Компьютерная графика - 3D-преобразования вращения
Вращение в 3D имеет больше нюансов по сравнению с преобразованием вращения в 2D, так как в 3D-вращении мы имеем дело с 3-мя осями (x, y, z).
Вращение вокруг произвольной оси
Есть три вида произвольного вращения, здесь мы можем вращать объект параллельно (или вдоль) определенной оси, так что координата, вокруг которой вращается объект, остается неизменной, а остальные две координаты изменяются. Возможны три вида таких поворотов :
- Вращение вокруг оси X,
- Вращение вокруг оси Y,
- Вращение вокруг оси Z.
1) Вращение вокруг оси x: В этом виде вращения объект вращается параллельно оси x (главной оси) , где координата x остается неизменным, а остальные две координаты y и z изменяются только. Рассмотрим точку с начальной координатой P (x, y, z) в трехмерном пространстве, которая вращается параллельно главной оси (оси x). Координатное положение изменится на P '(x, y, z).
Матрица преобразования вращения используется для вычисления новой координаты положения P ', которая показана ниже:
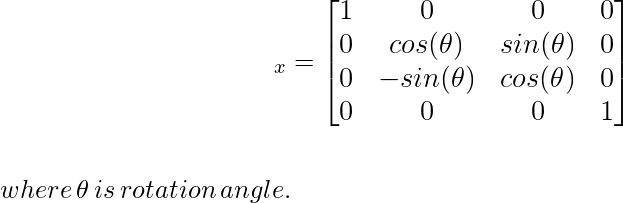


Вращение по оси x
2) Вращение вокруг оси Y: при таком вращении объект вращается параллельно оси Y (главной оси), где координата y остается неизменной, а остальные две координаты x и z изменяются только.
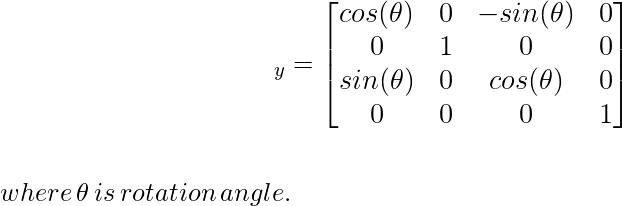

Вращение по оси Y
Рассмотрим точку с начальной координатой P (x, y, z) в трехмерном пространстве, которая вращается параллельно главной оси (оси y). Координатное положение изменится на P '(x, y, z).
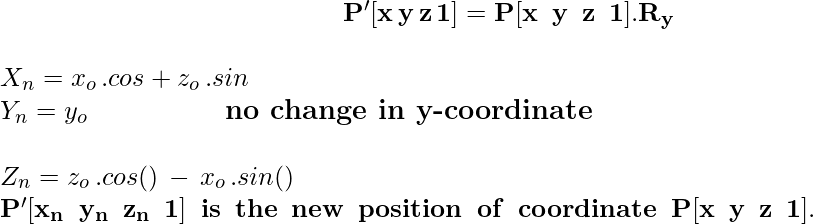
3) Вращение вокруг оси z: при таком вращении объект вращается параллельно оси z (главной оси) , где координата z остается неизменной, а остальные две координаты x и y изменяются только. 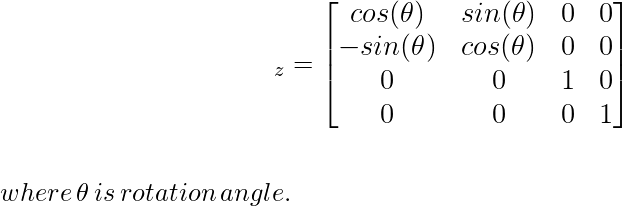
Рассмотрим точку с начальной координатой P (x, y, z) в трехмерном пространстве, которая вращается параллельно главной оси (оси y). Координатное положение изменится на P '(x, y, z).
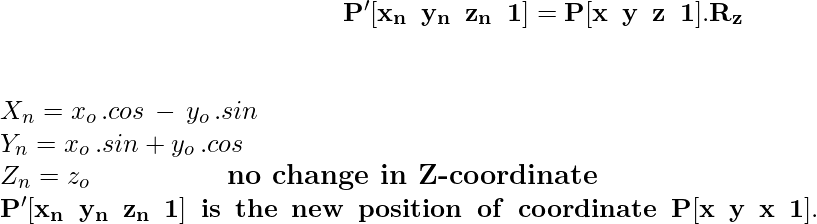
Примечание. Угол поворота в направлении против часовой стрелки всегда считается + ve, в то время как угол поворота по часовой стрелке всегда считается -ve. Это общепринятое соглашение, которому всегда следуют при трехмерном вращении.
Выполните преобразование «Поворот» над кубом OABCDEFG и поверните его на 45 * против часовой стрелки вокруг оси y.
Нам дан следующий рисунок:

Рисунок 1
Теперь мы применим трансформацию вращения вдоль (параллельно) оси y, которая:
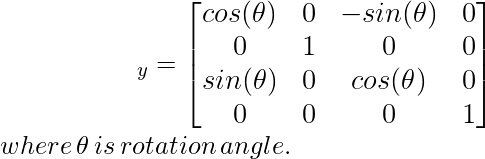
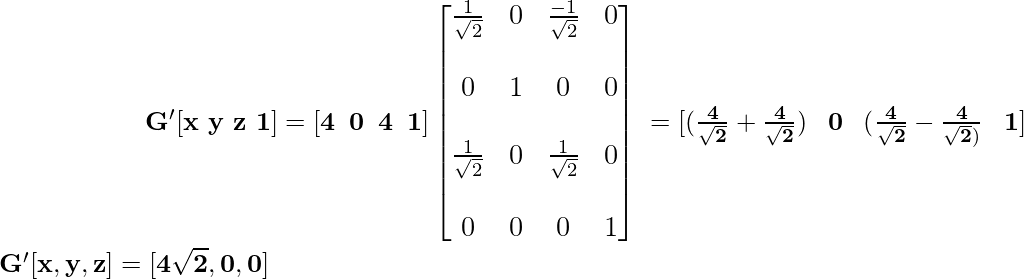
Координата O после применения преобразования вращения становится:
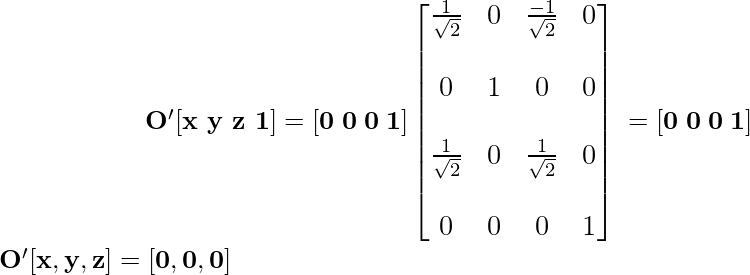
Координата A после применения преобразования вращения становится:

Координата B после применения преобразования вращения становится:
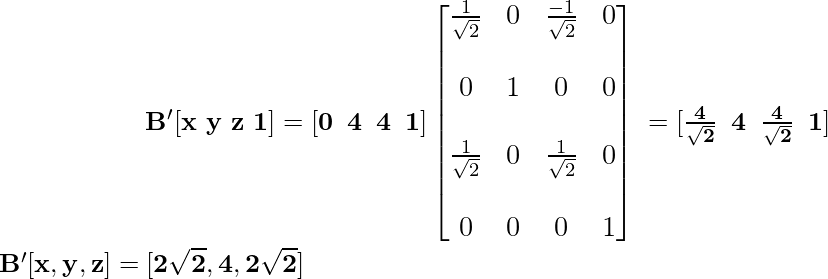
Координата C после применения преобразования вращения становится:
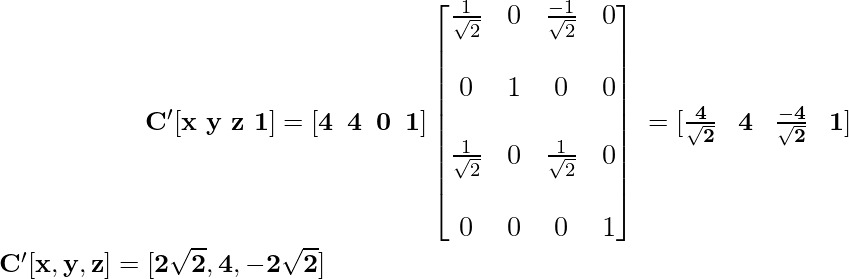
Координата D после применения преобразования вращения принимает вид:
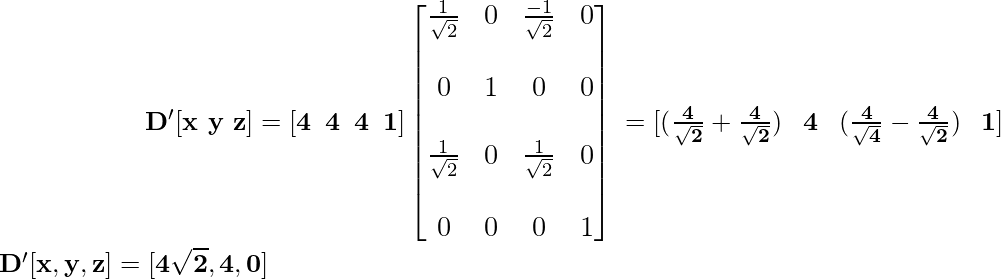
Координата E после применения преобразования вращения принимает вид:
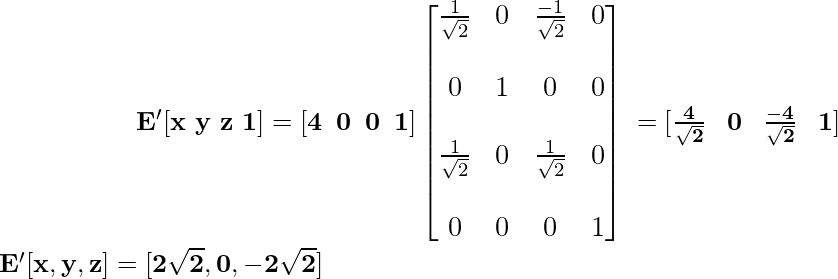
Координата F после применения преобразования вращения принимает вид:
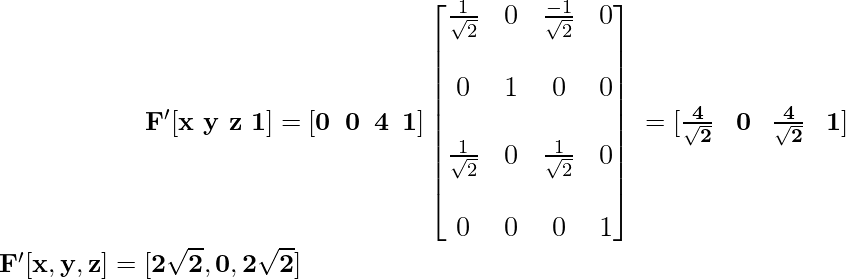
Координата G после применения преобразования вращения становится:
Итак, куб, который мы получим после успешного выполнения вращательного преобразования куба OABCDEF, будет выглядеть так:

Вниманию читателя! Не переставай учиться сейчас. Ознакомьтесь со всеми важными концепциями теории CS для собеседований по SDE с помощью курса теории CS по доступной для студентов цене и будьте готовы к работе в отрасли.