Гиперплоскость, подпространство и полупространство

1. Гиперплоскость:
Геометрически гиперплоскость - это геометрический объект, размерность которого на единицу меньше, чем окружающее пространство.

Что это значит?
Это означает следующее. Например, если вы возьмете трехмерное пространство, тогда гиперплоскость - это геометрический объект, который безразмерен на единицу. Таким образом, он будет двухмерным, а двухмерный объект в трехмерном пространстве будет плоскостью. Теперь, если вы возьмете 2 измерения, то одно безразмерное будет одномерным геометрическим объектом, которым будет линия и так далее.

• Гиперплоскость обычно описывается следующим уравнением

  Х ^Т п + Ь = 0

• Если мы расширим это до n переменных, мы получим что-то вроде этого

  X ₁ n ₁ + X ₂ n ₂ + X ₃ n ₃ + ……… .. + X _n n _n + b = 0

• Всего в двух измерениях мы получим нечто подобное, которое представляет собой не что иное, как уравнение линии.

  Икс ₁ N ₁ + Х ₂ N ₂ + Ь = 0

Пример:

Рассмотрим 2D-геометрию с

Хотя это 2D-геометрия, значение X будет

Таким образом, согласно уравнению гиперплоскости его можно решить как

Итак, как вы можете видеть из решения, гиперплоскость - это уравнение прямой. 

2. Подпространство:
Гиперплоскости, вообще говоря, не подпространства. Однако, если у нас есть гиперплоскости вида,

X ^T n = 0

То есть, если плоскость проходит через начало координат, то гиперплоскость также становится подпространством.

3. Полупространство:
Рассмотрим это двухмерное изображение, приведенное ниже.

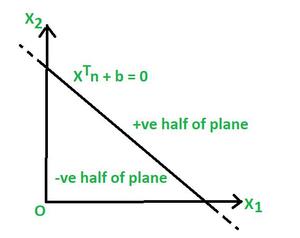
Итак, здесь у нас есть 2-мерное пространство в X ₁ и X _2, и, как мы обсуждали ранее, уравнение в двух измерениях будет линией, которая будет гиперплоскостью. Итак, уравнение линии записывается как

Х ^Т п + Ь = 0

Итак, для этих двух измерений мы могли бы написать эту строку, как мы обсуждали ранее

Икс ₁ N ₁ + Х ₂ N ₂ + Ь = 0

Вы можете заметить из приведенного выше графика, что все это двумерное пространство разбито на два пространства; Один на этой стороне (+ ve половина плоскости) линии, а другой на этой стороне (-ве половине плоскости) линии. Теперь эти два пространства называются полупространствами.

Пример:

Let’s consider the same example that we have taken in hyperplane case. So by solving, we got the equation as 

x₁ + 3x₂ + 4 = 0

There may arise 3 cases. Let’s discuss each case with an example.

Case 1:

x₁ + 3x₂ + 4 = 0 : On the line

Let consider two points (-1,-1). When we put this value on the equation of line we got 0. So we can say that this point is on the hyperplane of the line. 

Case 2: 
Similarly, 

x₁ + 3x₂ + 4 > 0 : Positive half-space

Consider two points (1,-1). When we put this value on the equation of line we got 2 which is greater than 0. So we can say that this point is on the positive half space. 
Case 3: 

x₁ + 3x₂ + 4 < 0 : Negative half-space

Consider two points (1,-2). When we put this value on the equation of line we got -1 which is less than 0. So we can say that this point is on the negative half-space.