Бинарный поиск

Опубликовано: 21 Января, 2022

Для отсортированного массива arr [] из n элементов напишите функцию для поиска данного элемента x в arr [].
Простой подход - выполнить линейный поиск . Временная сложность описанного выше алгоритма O (n). Другой подход к выполнению той же задачи - использование двоичного поиска.
Двоичный поиск: поиск в отсортированном массиве путем многократного деления интервала поиска пополам. Начните с интервала, охватывающего весь массив. Если значение ключа поиска меньше, чем значение в середине интервала, сузьте интервал до нижней половины. В противном случае сузьте его до верхней половины. Неоднократно проверяйте, пока значение не будет найдено или интервал не станет пустым.

Пример :

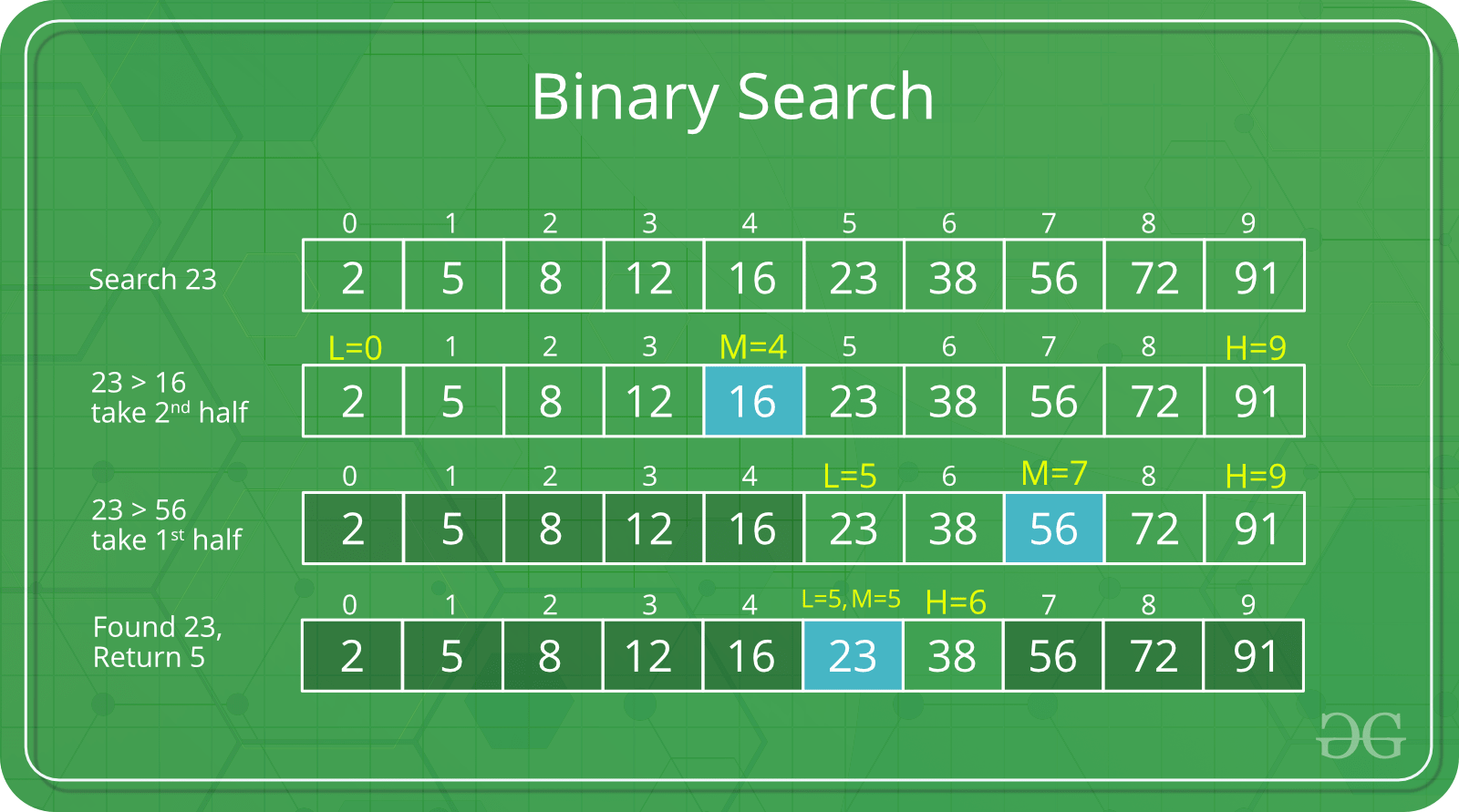
Идея двоичного поиска состоит в том, чтобы использовать информацию о том, что массив отсортирован, и уменьшить временную сложность до O (Log n).

Рекомендуется: сначала решите эту проблему на «ПРАКТИКЕ», прежде чем переходить к решению.

Мы практически игнорируем половину элементов сразу после одного сравнения.

  1. Сравните x со средним элементом.
  2. Если x соответствует среднему элементу, мы возвращаем средний индекс.
  3. Иначе Если x больше среднего элемента, то x может находиться только в правой половине подмассива после среднего элемента. Итак, мы возвращаемся к правой половине.
  4. Иначе (x меньше) повторяется для левой половины.

Recursive implementation of Binary Search 

C++

// C++ program to implement recursive Binary Search
#include <bits/stdc++.h>
using namespace std;
 
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
int binarySearch(int arr[], int l, int r, int x)
{
    if (r >= l) {
        int mid = l + (r - l) / 2;
 
        // If the element is present at the middle
        // itself
        if (arr[mid] == x)
            return mid;
 
        // If element is smaller than mid, then
        // it can only be present in left subarray
        if (arr[mid] > x)
            return binarySearch(arr, l, mid - 1, x);
 
        // Else the element can only be present
        // in right subarray
        return binarySearch(arr, mid + 1, r, x);
    }
 
    // We reach here when element is not
    // present in array
    return -1;
}
 
int main(void)
{
    int arr[] = { 2, 3, 4, 10, 40 };
    int x = 10;
    int n = sizeof(arr) / sizeof(arr[0]);
    int result = binarySearch(arr, 0, n - 1, x);
    (result == -1) ? cout << "Element is not present in array"
                   : cout << "Element is present at index " << result;
    return 0;
}

C

// C program to implement recursive Binary Search
#include <stdio.h>
 
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
int binarySearch(int arr[], int l, int r, int x)
{
    if (r >= l) {
        int mid = l + (r - l) / 2;
 
        // If the element is present at the middle
        // itself
        if (arr[mid] == x)
            return mid;
 
        // If element is smaller than mid, then
        // it can only be present in left subarray
        if (arr[mid] > x)
            return binarySearch(arr, l, mid - 1, x);
 
        // Else the element can only be present
        // in right subarray
        return binarySearch(arr, mid + 1, r, x);
    }
 
    // We reach here when element is not
    // present in array
    return -1;
}
 
int main(void)
{
    int arr[] = { 2, 3, 4, 10, 40 };
    int n = sizeof(arr) / sizeof(arr[0]);
    int x = 10;
    int result = binarySearch(arr, 0, n - 1, x);
    (result == -1) ? printf("Element is not present in array")
                   : printf("Element is present at index %d",
                            result);
    return 0;
}

Java

// Java implementation of recursive Binary Search
class BinarySearch {
    // Returns index of x if it is present in arr[l..
    // r], else return -1
    int binarySearch(int arr[], int l, int r, int x)
    {
        if (r >= l) {
            int mid = l + (r - l) / 2;
 
            // If the element is present at the
            // middle itself
            if (arr[mid] == x)
                return mid;
 
            // If element is smaller than mid, then
            // it can only be present in left subarray
            if (arr[mid] > x)
                return binarySearch(arr, l, mid - 1, x);
 
            // Else the element can only be present
            // in right subarray
            return binarySearch(arr, mid + 1, r, x);
        }
 
        // We reach here when element is not present
        // in array
        return -1;
    }
 
    // Driver method to test above
    public static void main(String args[])
    {
        BinarySearch ob = new BinarySearch();
        int arr[] = { 2, 3, 4, 10, 40 };
        int n = arr.length;
        int x = 10;
        int result = ob.binarySearch(arr, 0, n - 1, x);
        if (result == -1)
            System.out.println("Element not present");
        else
            System.out.println("Element found at index " + result);
    }
}
/* This code is contributed by Rajat Mishra */

Python3

# Python3 Program for recursive binary search.
 
# Returns index of x in arr if present, else -1
def binarySearch (arr, l, r, x):
 
    # Check base case
    if r >= l:
 
        mid = l + (r - l) // 2
 
        # If element is present at the middle itself
        if arr[mid] == x:
            return mid
         
        # If element is smaller than mid, then it
        # can only be present in left subarray
        elif arr[mid] > x:
            return binarySearch(arr, l, mid-1, x)
 
        # Else the element can only be present
        # in right subarray
        else:
            return binarySearch(arr, mid + 1, r, x)
 
    else:
        # Element is not present in the array
        return -1
 
# Driver Code
arr = [ 2, 3, 4, 10, 40 ]
x = 10
 
# Function call
result = binarySearch(arr, 0, len(arr)-1, x)
 
if result != -1:
    print ("Element is present at index % d" % result)
else:
    print ("Element is not present in array")

C#

// C# implementation of recursive Binary Search
using System;
 
class GFG {
    // Returns index of x if it is present in
    // arr[l..r], else return -1
    static int binarySearch(int[] arr, int l,
                            int r, int x)
    {
        if (r >= l) {
            int mid = l + (r - l) / 2;
 
            // If the element is present at the
            // middle itself
            if (arr[mid] == x)
                return mid;
 
            // If element is smaller than mid, then
            // it can only be present in left subarray
            if (arr[mid] > x)
                return binarySearch(arr, l, mid - 1, x);
 
            // Else the element can only be present
            // in right subarray
            return binarySearch(arr, mid + 1, r, x);
        }
 
        // We reach here when element is not present
        // in array
        return -1;
    }
 
    // Driver method to test above
    public static void Main()
    {
 
        int[] arr = { 2, 3, 4, 10, 40 };
        int n = arr.Length;
        int x = 10;
 
        int result = binarySearch(arr, 0, n - 1, x);
 
        if (result == -1)
            Console.WriteLine("Element not present");
        else
            Console.WriteLine("Element found at index "
                              + result);
    }
}
 
// This code is contributed by Sam007.

PHP

<?php
// PHP program to implement
// recursive Binary Search
 
// A recursive binary search
// function. It returns location
// of x in given array arr[l..r]
// is present, otherwise -1
function binarySearch($arr, $l, $r, $x)
{
if ($r >= $l)
{
        $mid = ceil($l + ($r - $l) / 2);
 
        // If the element is present
        // at the middle itself
        if ($arr[$mid] == $x)
            return floor($mid);
 
        // If element is smaller than
        // mid, then it can only be
        // present in left subarray
        if ($arr[$mid] > $x)
            return binarySearch($arr, $l,
                                $mid - 1, $x);
 
        // Else the element can only
        // be present in right subarray
        return binarySearch($arr, $mid + 1,
                            $r, $x);
}
 
// We reach here when element
// is not present in array
return -1;
}
 
// Driver Code
$arr = array(2, 3, 4, 10, 40);
$n = count($arr);
$x = 10;
$result = binarySearch($arr, 0, $n - 1, $x);
if(($result == -1))
echo "Element is not present in array";
else
echo "Element is present at index ",
                            $result;
                             
// This code is contributed by anuj_67.
?>

Javascript

<script>
// JavaScript program to implement recursive Binary Search
 
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is present,
// otherwise -1
function binarySearch(arr, l, r, x){
    if (r >= l) {
        let mid = l + Math.floor((r - l) / 2);
 
        // If the element is present at the middle
        // itself
        if (arr[mid] == x)
            return mid;
 
        // If element is smaller than mid, then
        // it can only be present in left subarray
        if (arr[mid] > x)
            return binarySearch(arr, l, mid - 1, x);
 
        // Else the element can only be present
        // in right subarray
        return binarySearch(arr, mid + 1, r, x);
    }
 
    // We reach here when element is not
    // present in array
    return -1;
}
 
let arr = [ 2, 3, 4, 10, 40 ];
let x = 10;
let n = arr.length
let result = binarySearch(arr, 0, n - 1, x);
(result == -1) ? document.write( "Element is not present in array")
                   : document.write("Element is present at index " +result);
</script>

Выход :

 Элемент присутствует в индексе 3

Здесь вы можете создать функцию проверки для упрощения реализации.

Here is recursive implementation with check function which I feel is a much easier implementation:

C++

C++
 
#include <bits/stdc++.h>
using namespace std;
 
//define array globally
const int N = 1e6 +4;
 
int a[N];
int n;//array size
 
//elememt to be searched in array
   int k;
 
bool check(int dig)
{
    //element at dig position in array
    int ele=a[dig];
 
    //if k is less than
    //element at dig position
    //then we need to bring our higher ending to dig
    //and then continue further
    if(k<=ele)
    {
        return 1;
    }
    else
    {
    return 0;
    }
}
void binsrch(int lo,int hi)
{
    while(lo<hi)
    {
        int mid=(lo+hi)/2;
        if(check(mid))
        {
            hi=mid;
        }
        else
        {
            lo=mid+1;
        }
    }
    //if a[lo] is k
    if(a[lo]==k)
        cout<<"Element found at index "<<lo;// 0 based indexing
    else
        cout<<"Element doesnt exist in array";//element was not in our array
 
}
 
 
int main()
{  
    cin>>n;
   for(int i=0; i<n; i++)
Oracle

РЕКОМЕНДУЕМЫЕ СТАТЬИ

Опыт собеседования OFSS для младшего консультанта FTE (на кампусе)
26 Января, 2023
Oracle Interview Experience для инженера по серверным технологиям (в кампусе) 2022 г.
26 Января, 2023
Oracle Interview Experience для разработки приложений FTE
26 Января, 2023
Oracle Interview Experience для младшего инженера-программиста (в кампусе) 2022 г.
26 Января, 2023
Oracle Interview Experience для Project Intern (в кампусе) 2021 г.
26 Января, 2023
Oracle Interview Experience для SDE 2022
25 Января, 2023
Oracle Interview Experience для OFSS и GBU (в кампусе)
25 Января, 2023
Oracle Interview Experience для младшего инженера-программиста
25 Января, 2023