Архитектура и процесс обучения в нейронной сети

Чтобы узнать об обратном распространении , мы сначала должны понять архитектуру нейронной сети, а затем процесс обучения в ИНС. Итак, давайте начнем с знакомства с различными архитектурами ИНС:

Архитектуры нейронной сети:

ИНС - это вычислительная система, состоящая из множества взаимосвязанных единиц, называемых искусственными нейронами . Связь между искусственными нейронами может передавать сигнал от одного нейрона к другому. Итак, есть несколько возможностей для подключения нейронов, в зависимости от архитектуры, которую мы собираемся принять для конкретного решения. Вот некоторые перестановки и комбинации:

• В сети может быть всего два слоя нейронов - входной и выходной.
• В нейроне может быть один или несколько промежуточных «скрытых» слоев.
• Нейроны могут быть связаны со всеми нейронами следующего слоя и так далее ...

Итак, давайте поговорим о различных возможных архитектурах:

A. Однослойная прямая сеть:

Это самая простая и базовая архитектура ИНС. Он состоит всего из двух слоев - входного и выходного. Входной слой состоит из m входных нейронов, подключенных к каждому из n выходных нейронов. Соединения имеют вес w ₁₁ и т. Д. Входной слой нейронов не выполняет никакой обработки - они передают i / p-сигналы нейронам o / p. Вычисления выполняются в выходном слое. Итак, хотя он имеет 2 слоя нейронов, только один слой выполняет вычисления. Это причина того, что сеть известна как ОДИН уровень. Кроме того, сигналы всегда текут от входного уровня к выходному слою. Следовательно, сеть известна как FEED FORWARD.

Чистый сигнал, поступающий на выходные нейроны, определяется следующим образом:

Выходной сигнал каждого выходного нейрона будет зависеть от используемой функции активации.

Б. Многослойная прямая сеть:

Многослойная прямая сеть

Многослойная сеть с прямой связью очень похожа на однослойную сеть с прямой связью, за исключением того факта, что между входным и выходным слоями есть один или несколько промежуточных слоев нейронов. Следовательно, сеть называется многослойной. Каждый из слоев может иметь различное количество нейронов. Например, показанный на диаграмме выше имеет m нейронов во входном слое и r нейронов в выходном слое, и есть только один скрытый слой с n нейронами.

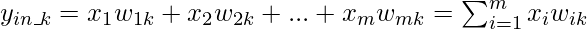
для k-го нейрона скрытого слоя. Чистый сигнал, поступающий в нейрон в выходном слое, определяется как:

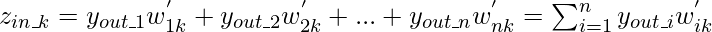
C. Конкурентная сеть:

По структуре она такая же, как и у однослойной сети с прямой связью. Единственное отличие состоит в том, что выходные нейроны связаны друг с другом (частично или полностью) . Ниже представлена диаграмма для этого типа сети.

Конкурентная сеть

По диаграмме видно, что несколько выходных нейронов связаны друг с другом. Для заданного входа выходные нейроны конкурируют друг с другом за представление входных данных. Он представляет собой форму алгоритма обучения без учителя в ИНС, который подходит для поиска кластеров в наборе данных.

D. Рекуррентная сеть:

Рекуррентная сеть

В сетях с прямой связью сигнал всегда течет от входного уровня к выходному (только в одном направлении). В случае рекуррентных нейронных сетей существует петля обратной связи (от нейронов выходного слоя к нейронам входного слоя). Могут быть и петли.

Процесс обучения в ИНС:

Процесс обучения в ИНС в основном зависит от четырех факторов, а именно:

1. Количество слоев в сети (однослойный или многослойный)
2. Направление потока сигнала (прямая или рекуррентная)
3. Количество узлов в слоях: количество узлов во входном слое равно количеству функций входного набора данных. Количество выходных узлов будет зависеть от возможных результатов, т.е. количества классов в случае обучения с учителем. Но количество слоев в скрытом слое выбирается пользователем. Чем больше количество узлов на скрытом уровне, тем выше производительность, но слишком много узлов может привести к переобучению, а также к увеличению вычислительных затрат.
4. Вес взаимосвязанных узлов: определение значения весов, присваиваемых каждому взаимодействию между каждым нейроном, так что конкретная проблема обучения может быть решена правильно, сама по себе является довольно сложной задачей. Возьмем пример, чтобы понять проблему. Возьмем пример многослойной сети прямого распространения, мы должны обучить модель ИНС, используя некоторые данные, чтобы она могла классифицировать новый набор данных, скажем п_5 (3, -2). Скажем, мы вывели, что p_1 = (5,2) и p_2 = (-1,12) принадлежат классу C1, тогда как p_3 = (3, -5) и p_4 = (-2, -1) принадлежат классу C2. Мы принимаем значения синаптических весов w_0, w_1, w_2 равными -2, 1/2 и 1/4 соответственно. Но мы НЕ будем получать эти значения веса для каждой учебной задачи. Для решения проблемы обучения с помощью ИНС мы можем начать с набора значений синаптических весов и продолжать изменять их на нескольких итерациях. Критерием остановки может быть степень ошибочной классификации <1% или максимальное количество итераций должно быть меньше 25 (пороговое значение). Может возникнуть еще одна проблема: процент ошибочной классификации не может постепенно снижаться.

Итак, мы можем резюмировать процесс обучения в ИНС как комбинацию - определения количества скрытых слоев, количества узлов в каждом из скрытых слоев, направления потока сигнала, определения веса соединения.

Многослойная питающая сеть - это широко используемая архитектура. Было замечено, что нейронная сеть даже с одним скрытым слоем может использоваться для разумной аппроксимации любой непрерывной функции. Методология обучения, принятая для обучения многослойной сети с прямой связью, называется Backpropagation.

Обратное распространение:

В приведенном выше разделе мы узнаем, что наиболее важными действиями при обучении ИНС являются присвоение весов межнейронных связей. В 1986 году был представлен эффективный способ обучения ИНС. В этом методе разница в выходных значениях выходного слоя и ожидаемых значениях распространяется обратно из выходного слоя на предыдущие уровни. Следовательно, алгоритм, реализующий этот метод, известен как ОБРАТНОЕ РАСПРОСТРАНЕНИЕ, т.е. распространение ошибок обратно на предыдущие уровни.

Алгоритм обратного распространения ошибки применим для многослойной сети с прямой связью. Это контролируемый алгоритм обучения, который продолжает регулировать веса подключенных нейронов с целью уменьшить отклонение выходного сигнала от целевого. Этот алгоритм состоит из нескольких итераций, известных как эпохи. Каждая эпоха состоит из двух фаз:

• Прямая фаза: поток сигнала от нейронов входного слоя к нейронам выходного слоя через скрытые слои. Веса взаимосвязей и функций активации используются во время потока. В выходном слое генерируются выходные сигналы.
• Обратная фаза: сигнал сравнивается с ожидаемым значением. Вычисленные ошибки распространяются в обратном направлении от вывода к предыдущему уровню. Возвратные ошибки используются для корректировки весов взаимосвязей между слоями.

ОБРАТНАЯ СВЯЗЬ

На приведенной выше диаграмме изображена достаточно упрощенная версия алгоритма обратного распространения.

Одна из основных частей алгоритма - это корректировка весов межсоединений. Это делается с помощью техники, называемой градиентным спуском . Проще говоря, алгоритм вычисляет частную производную функции активации по каждому весу межсоединения, чтобы определить «градиент» или степень изменения веса, необходимого для минимизации функции стоимости.

Чтобы подробно понять алгоритм обратного распространения, давайте рассмотрим многослойную прямую сеть.

Чистый сигнал, поступающий на нейроны скрытого слоя, определяется следующим образом:

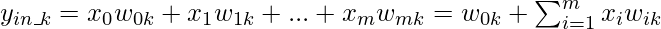
Если 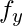- функция активации скрытого слоя, то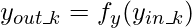

Чистый сигнал, поступающий на нейроны выходного слоя, определяется выражением:

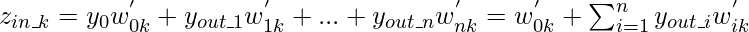
ОБРАТНАЯ СЕТЬ

Обратите внимание, что сигналы 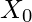а также 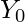считаются равными 1. Если 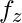- функция активации скрытого слоя, то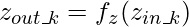

Если является целью k-го выходного нейрона, то функция стоимости, определяемая как квадрат ошибки выходного слоя, определяется следующим образом:

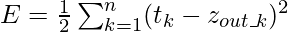
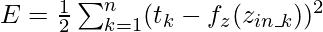
Согласно алгоритму спуска , необходимо взять частную производную функции стоимости E по весам межсоединений. Математически это можно представить как:

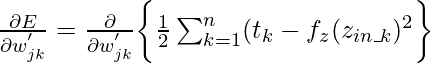
{Вышеупомянутое выражение предназначено для весов взаимосвязей между j-м нейроном в скрытом слое и k-м нейроном в выходном слое .} Это выражение может быть сокращено до

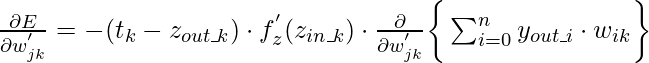
где, 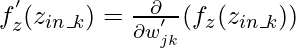или же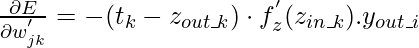

Если мы предположим 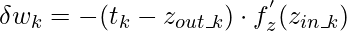как компонент регулировки веса, необходимой для веса 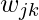соответствующий k-му выходному нейрону, то:

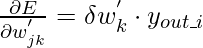
Исходя из этого, веса и смещение необходимо обновить следующим образом:

• Для весов:
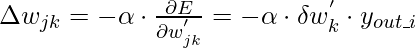
• Следовательно,
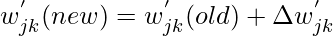
• Для предвзятости:
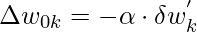
• Следовательно,

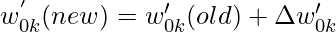
В приведенных выше выражениях альфа - это скорость обучения нейронной сети. Скорость обучения - это пользовательский параметр, который уменьшает или увеличивает скорость, с которой должны корректироваться веса межсоединений нейронной сети. Если скорость обучения слишком высока, регулировка, выполняемая как часть процесса градиентного спуска, может привести к отклонению набора данных, а не к его схождению. С другой стороны, если скорость обучения слишком низкая, оптимизация может занять больше времени из-за небольших шагов к минимумам.

{Все приведенные выше вычисления относятся к весу взаимосвязи между нейронами в скрытом слое и нейронами в выходном слое}

Подобно приведенным выше выражениям, мы можем вывести выражения для «Веса взаимосвязи между входным и скрытым слоями:

• Для весов:
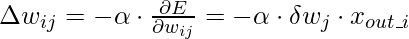
• Следовательно,
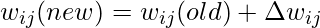
• Для предвзятости:
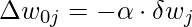
• Следовательно,

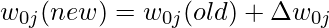
Таким образом, мы можем использовать алгоритм Backpropagation для решения различных искусственных нейронных сетей.