Z-тест

Опубликовано: 17 Июля, 2021

Z-тест - это статистический метод, позволяющий определить, может ли распределение статистики теста быть аппроксимировано нормальным распределением. Это метод определения того, являются ли два средних значения выборки примерно одинаковыми или разными, если известна их дисперсия и размер выборки большой (должен быть> = 30).

Когда использовать Z-тест:

  • Размер выборки должен быть больше 30. В противном случае следует использовать t-критерий.
  • Выборки следует отбирать случайным образом из совокупности.
  • Следует знать стандартное отклонение генеральной совокупности.
  • Выборки, взятые из совокупности, должны быть независимыми друг от друга.
  • Данные должны быть нормально распределены, однако для большого размера выборки предполагается, что они имеют нормальное распределение.

Проверка гипотезы

Гипотеза - это обоснованное предположение / утверждение об определенном свойстве объекта. Проверка гипотез - это способ подтвердить утверждение эксперимента.

  • Нулевая гипотеза: Нулевая гипотеза - это утверждение, что значение параметра совокупности (например, пропорции, среднего или стандартного отклонения) равно некоторому заявленному значению. Мы либо отвергаем, либо не можем отвергнуть нулевую гипотезу. Нулевая гипотеза обозначается H 0 .
  • Альтернативная гипотеза: альтернативная гипотеза - это утверждение, что параметр имеет значение, отличное от заявленного. Обозначается H A.

Уровень значимости: означает степень значимости, при которой мы принимаем или отвергаем нулевую гипотезу. Поскольку в большинстве экспериментов стопроцентная точность невозможна для принятия или отклонения гипотезы, поэтому мы выбираем уровень значимости. Обозначается он альфа (∝) .

Шаги для выполнения Z-теста:

  • Сначала определите нулевую и альтернативную гипотезы.
  • Определите уровень значимости (∝).
  • Найдите критическое значение z в z-тесте, используя
  • Рассчитайте статистику z-теста. Ниже приведена формула для расчета статистики z-теста.

  • где,
    • X¯: среднее значение выборки.
    • Му: среднее значение населения.
    • Sd: стандартное отклонение генеральной совокупности.
    • n: размер выборки.
  • Теперь сравните с гипотезой и решите, отвергать или нет нулевую гипотезу.

Тип Z-теста

  • Левосторонний тест: в этом тесте наша область отклонения находится в крайнем левом углу распределения. Здесь наша нулевая гипотеза состоит в том, что заявленное значение меньше или равно среднему значению для генеральной совокупности.

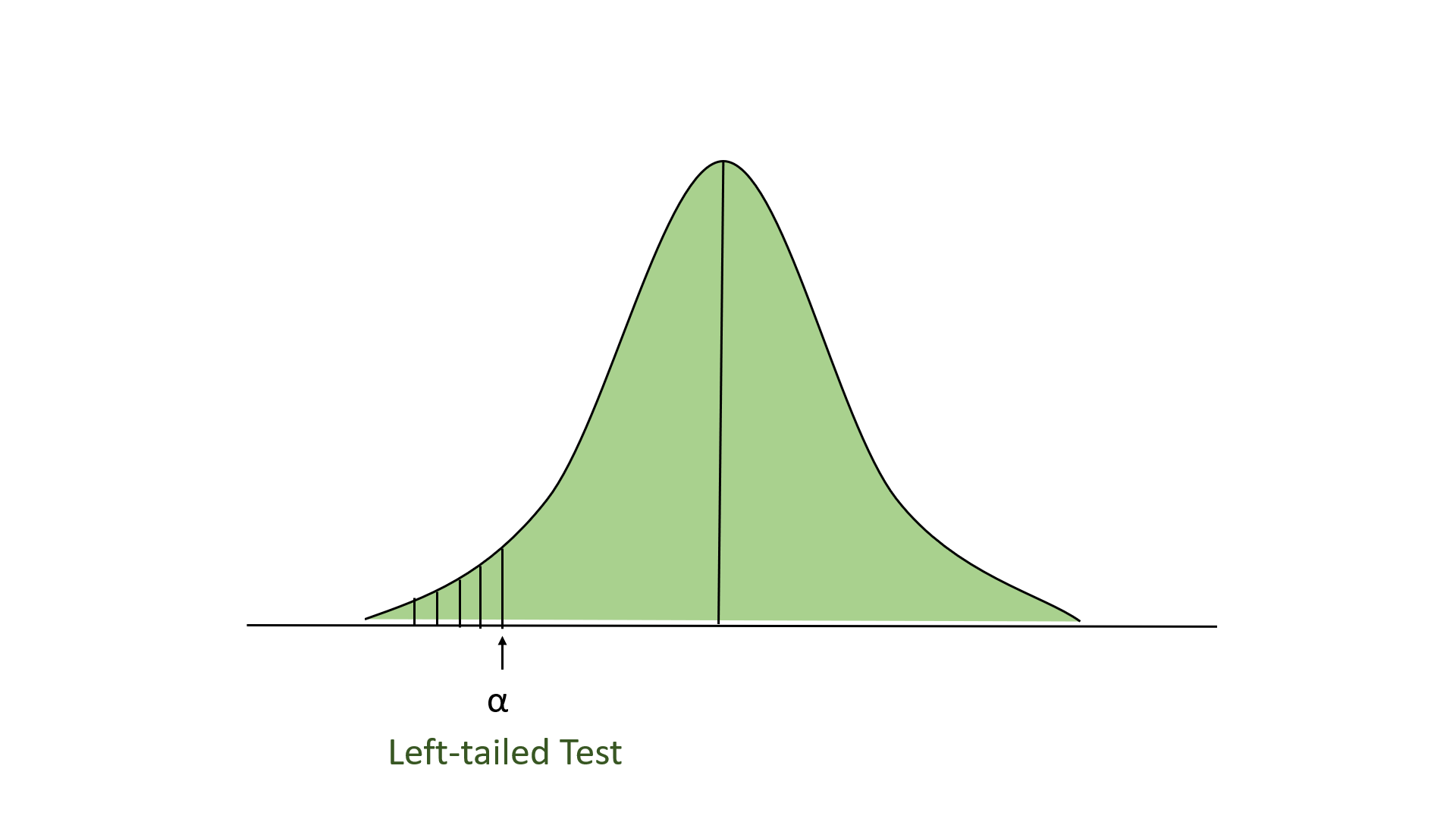
  • Правосторонний тест: в этом тесте наша область отклонения находится в крайнем правом углу распределения. Здесь наша нулевая гипотеза состоит в том, что заявленное значение меньше или равно среднему значению для генеральной совокупности.

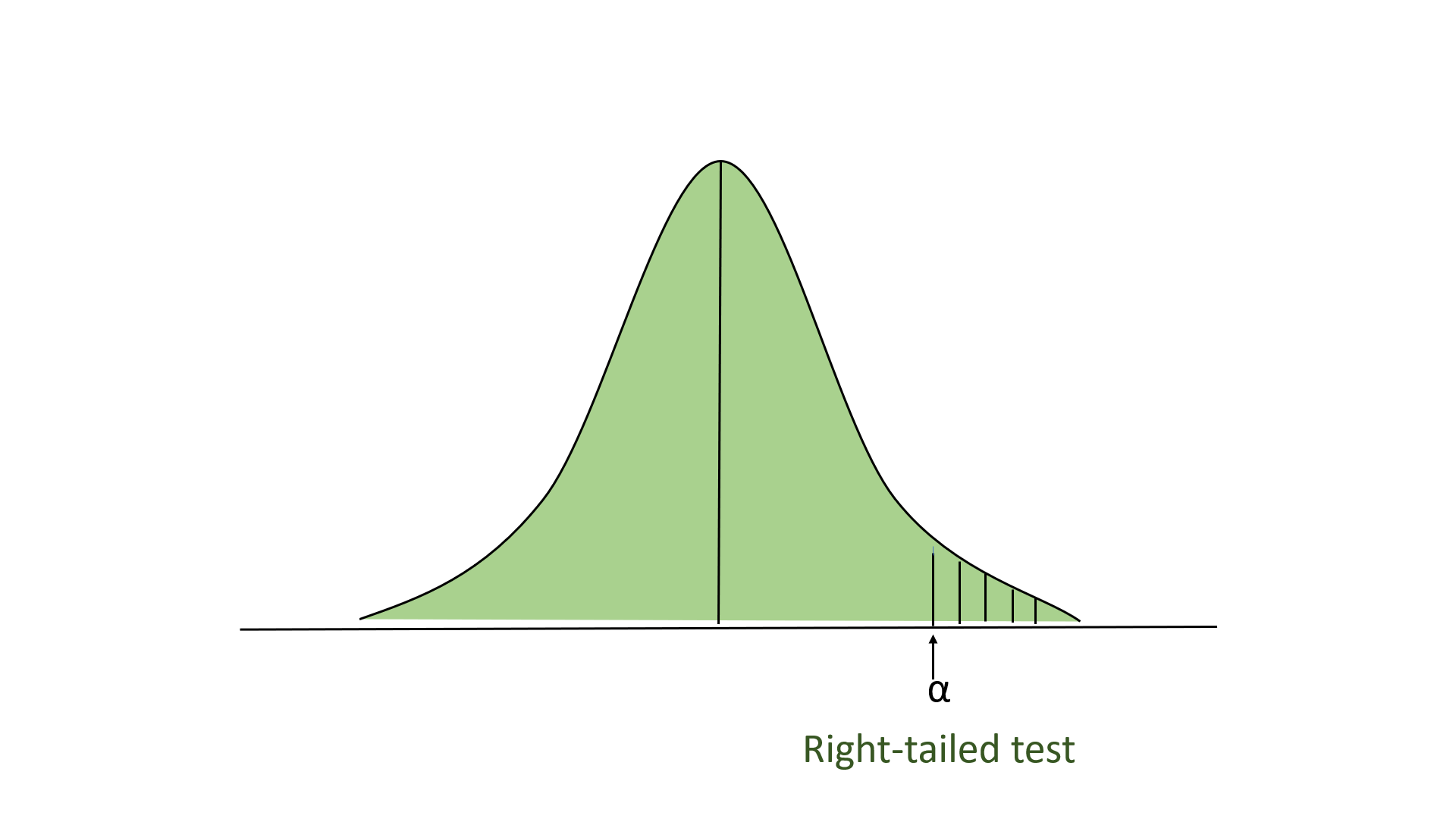
  • Двусторонний тест: в этом тесте наша область отклонения находится в обеих крайних точках распределения. Здесь наша нулевая гипотеза состоит в том, что заявленное значение равно среднему значению для совокупности.

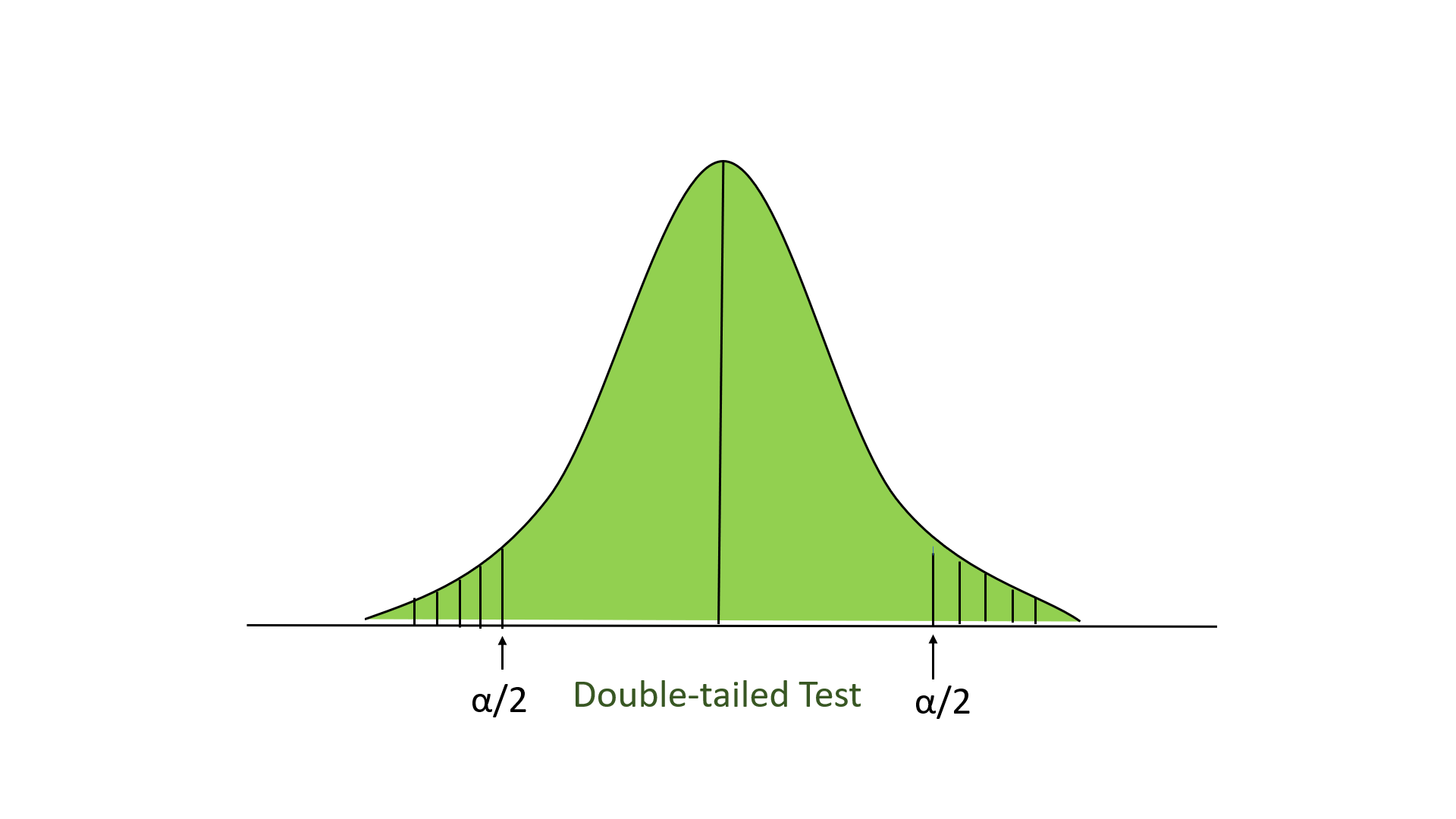
Ниже приведен пример выполнения z-теста:

Проблема : школа утверждала, что ученики учатся более умно, чем в средней школе. При подсчете баллов IQ 50 студентов среднее значение оказалось равным 11. Среднее значение IQ популяции составляет 100, а стандартное отклонение - 15. Укажите, является ли утверждение директора школы правильным или нет на уровне значимости 5%.

  • Сначала мы определяем нулевую гипотезу и альтернативную гипотезу. Наша нулевая гипотеза будет следующей:

и наша альтернативная гипотеза.

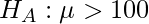
  • Укажите уровень значимости. Здесь наш уровень значимости, указанный в этом вопросе (∝ = 0,05), если не указан, то мы берем = 0,05.
  • Теперь посмотрим на z-таблицу. Для значения = 0,05 z-оценка для правостороннего теста составляет 1,645.
  • Теперь мы проводим Z-тест по проблеме:

  • Где:
    • Х = 110
    • Среднее (mu) = 100
    • Стандартное отклонение (сигма) = 15
    • Уровень значимости (альфа) = 0,05
    • n = 50

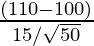
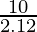
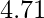
  • Здесь 4,71> 1,645, поэтому мы отвергаем нулевую гипотезу. Если статистика z-критерия меньше, чем z-score, мы не будем отвергать нулевую гипотезу.

Python3




# imports
import math
import numpy as np
from numpy.random import randn
from statsmodels.stats.weightstats import ztest
# Generate a random array of 50 numbers having mean 110 and sd 15
# similar to the IQ scores data we assume above
mean_iq = 110
sd_iq = 15 / math.sqrt( 50 )
alpha = 0.05
null_mean = 100
data = sd_iq * randn( 50 ) + mean_iq
# print mean and sd
print ( 'mean=%.2f stdv=%.2f' % (np.mean(data), np.std(data)))
# now we perform the test. In this function, we passed data, in value parameter
# we passed mean value in the null hypothesis, in alternative hypothesis we check whether the
# mean is larger
ztest_Score, p_value = ztest(data,value = null_mean, alternative = 'larger' )
# the function outputs a p_value and z-score corresponding to that value, we compare the
# p-value with alpha, if it is greater than alpha then we do not null hypothesis
# else we reject it.
if (p_value < alpha):
print ( "Reject Null Hypothesis" )
else :
print ( "Fail to Reject NUll Hypothesis" ) 
 Отклонить нулевую гипотезу

Двухвыборочный z-тест:
В этом тесте мы предоставили 2 нормально распределенные и независимые популяции, и мы произвольно отобрали выборки из обеих популяций. Здесь мы считаем u 1 и u 2 средними по генеральной совокупности, X 1 и X 2 - наблюдаемыми средними по выборке. Здесь наша нулевая гипотеза может быть такой:
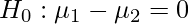
и альтернативная гипотеза
и формула для расчета оценки z-теста:
где сигма 1 и сигма 2 - стандартное отклонение, а n 1 и n 2 - размер выборки населения, соответствующий u 1 и u 2 .
Ошибка типа 1 и ошибка типа II:
  •  Ошибка типа I: ошибка типа 1 произошла, когда мы отклоняем нулевую гипотезу, даже если гипотеза верна. Эта ошибка обозначается альфой.
  •  Ошибка типа II: ошибка типа II возникла, когда мы не отвергли нулевую гипотезу, даже если гипотеза ложна. Эта ошибка обозначается бета-версией.
 Нулевая гипотеза верна Нулевая гипотеза ЛОЖНА
 Отклонить нулевую гипотезу
 Ошибка типа I
 (Ложно положительный)
 Правильное решение
 Неспособность отвергнуть нулевую гипотезу Правильное решение
 Ошибка типа II
 (Ложноотрицательный)

            

                            

                    
                                            Машинное обучение
                                    

                        

                
РЕКОМЕНДУЕМЫЕ СТАТЬИ

                

                                            

                            
Оживление фото: возможности и перспективы

                            
23 Мая, 2023

                        

                                            

                            
Линейный классификатор в Tensorflow

                            
21 Февраля, 2023

                        

                                            

                            
Обнаружение рака кожи с помощью TensorFlow

                            
21 Февраля, 2023

                        

                                            

                            
Прогнозирование цены Dogecoin с помощью машинного обучения

                            
21 Февраля, 2023

                        

                                            

                            
Прогнозирование права на получение ссуды с использованием моделей машинного обучения в Python

                            
21 Февраля, 2023

                        

                                            

                            
Сегментация клиентов с использованием неконтролируемого машинного обучения в Python

                            
14 Февраля, 2023

                        

                                            

                            
Распознавание дорожных знаков с использованием CNN и Keras в Python

                            
14 Февраля, 2023

                        

                                            

                            
Прогнозирование топливной эффективности с использованием Tensorflow в Python

                            
14 Февраля, 2023