Выравнивание гистограммы в цифровой обработке изображений

Цифровое изображение представляет собой двумерную матрицу двух пространственных координат, каждая ячейка которой определяет уровень интенсивности изображения в этой точке. Итак, у нас есть матрица N x N с целочисленными значениями в диапазоне от минимального уровня интенсивности 0 до максимального уровня L-1, где L обозначает количество уровней интенсивности. Следовательно, уровни интенсивности пикселя r могут принимать значения от 0,1,2,3,…. (Л-1). Как правило, L = 2 ^m , где m — количество битов, необходимых для представления уровней интенсивности. Интенсивность нулевого уровня означает полностью черный или темный цвет, тогда как уровень L-1 указывает на полностью белый цвет или отсутствие оттенков серого.

Преобразование интенсивности:

Преобразование интенсивности — это базовый метод обработки цифровых изображений, при котором уровни интенсивности пикселей изображения преобразуются в новые значения с использованием функции математического преобразования, чтобы получить новое выходное изображение. По сути, преобразования интенсивности просто реализуют следующую функцию:

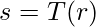
где s — новый уровень интенсивности пикселей, r — исходное значение интенсивности пикселей данного изображения, а r≥0.

При разных формах функции преобразования T(r) мы получаем разные выходные изображения.

Общие функции преобразования интенсивности:

1. Инверсия изображения. Инвертирует оттенки серого в изображении, делая темные пиксели более белыми, а белые — темнее. Это полностью аналогично фотонегативу, отсюда и название.

2. Преобразование журнала: здесь c — некоторая константа. Он используется для расширения значений темных пикселей в изображении.

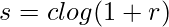
3. Степенное преобразование. Здесь c и γ — произвольные константы. Это преобразование можно использовать для различных целей, изменяя значение γ .

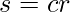
Выравнивание гистограммы:

Гистограмма цифрового изображения с уровнями интенсивности от 0 до (L-1) представляет собой функцию h( _rk ) = n _k , где _rk — это k-й уровень интенсивности, а n _k — количество пикселей в изображении, имеющих этот уровень интенсивности. Мы также можем нормализовать гистограмму, разделив ее на общее количество пикселей в изображении. Для изображения N x N у нас есть следующее определение нормализованной функции гистограммы:

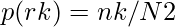
Эта функция p( _rk ) представляет собой вероятность появления пикселя с уровнем интенсивности _rk . Четко,

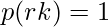
Гистограмма изображения, как показано на рисунке, состоит из оси x, представляющей уровни интенсивности _rk, и оси y, обозначающей функции h( _rk ) или p( _rk ) .

Гистограмма изображения дает важную информацию о оттенках серого и контрастности изображения. Если вся гистограмма изображения центрирована по направлению к левому концу оси x, то это подразумевает темное изображение. Если гистограмма больше наклонена к правому краю, это означает белое или яркое изображение. График гистограммы с узкой шириной в центре оси интенсивности показывает низкоконтрастное изображение, поскольку оно имеет несколько уровней оттенков серого. С другой стороны, равномерно распределенная гистограмма по всей оси X придает изображению эффект высокой контрастности.

При обработке изображений часто возникает необходимость улучшить контрастность изображения. В таких случаях мы используем метод преобразования интенсивности, известный как выравнивание гистограммы. Выравнивание гистограммы — это процесс равномерного распределения гистограммы изображения по всей оси интенсивности путем выбора соответствующей функции преобразования интенсивности. Следовательно, выравнивание гистограммы представляет собой процесс преобразования интенсивности.

Ниже математически объясняется выбор идеальной функции преобразования для равномерного распределения гистограммы изображения.

Математический вывод функции преобразования для выравнивания гистограммы:

Будем считать, что уровни интенсивности изображения r непрерывны, в отличие от дискретного случая в цифровых изображениях. Мы ограничиваем значения, которые может принимать r, между 0 и L-1, то есть 0 ≤ r ≤ L-1 . r = 0 представляет черный цвет, а r = L-1 представляет белый цвет. Рассмотрим произвольную функцию преобразования:

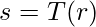
где s обозначает уровни интенсивности результирующего изображения. У нас есть определенные ограничения на T(r) .

• T(r) должна быть строго возрастающей функцией. Это делает ее инъективной функцией.
• 0 ≤ Т( г ) ≤ L-1. Это делает T(r) сюръективным.

Два вышеуказанных условия делают T(r) биективной функцией. Мы знаем, что такие функции обратимы. Таким образом, мы можем получить значения r из s. У нас может быть функция такая, что r = T-1( s )

Давайте теперь скажем, что функция плотности вероятности (PDF) r равна p _r (x) , а кумулятивная функция распределения (CDF) r равна F _r (x) . Теперь CDF s будет:

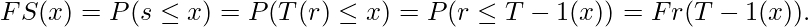
Мы ставим первое условие T(r) именно для того, чтобы предыдущий шаг был верным. Второе условие необходимо, так как s — это значение интенсивности для выходного изображения, поэтому оно должно быть между o и (L-1).

Таким образом, PDF s может быть получен путем дифференцирования F _S ( x ) по x . Получаем следующее соотношение:

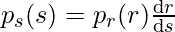
Теперь, если мы определим функцию преобразования следующим образом:

Затем использование этой функции дает нам равномерную PDF для s .

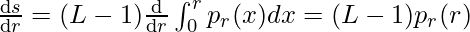
В приведенном выше шаге использовалось интегральное правило Лейбница. Используя приведенную выше производную, мы получаем:

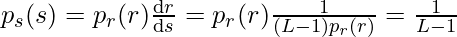
Таким образом, PDF s является однородным. Это то, чего мы хотим.

Теперь мы расширим описанный выше непрерывный случай до дискретного случая. Естественной заменой знака интеграла является суммирование. Следовательно, у нас остается следующая функция преобразования выравнивания гистограммы.

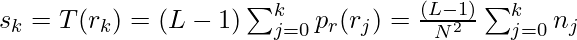
Поскольку s должно иметь целые значения, любое нецелое значение, полученное из приведенной выше функции, округляется до ближайшего целого числа.

Пример 1:

Выход:

Пример 2:

Выход: