U-тест Манна и Уитни

Опубликовано: 17 Июля, 2021

U-критерий Манна и Уитни или критерий суммы рангов Уилкоксона - это тест гипотезы непараметрической статистики, который используется для анализа разницы между двумя независимыми выборками порядковых данных. В этом тесте мы предоставили две случайно выбранные выборки, и мы должны проверить, принадлежат ли эти две выборки к одной и той же генеральной совокупности.

Допущение для U-критерия Манна-Уитни:

Все наблюдения обеих групп независимы друг от друга.
Значения зависимой переменной должны быть упорядочены (это означает, что их можно сравнивать друг с другом и ранжировать в порядке от наибольшего к наименьшему).
Независимая переменная должна быть двумя независимыми категориальными группами.
Для каждого образца рекомендуемое число от 5 до 20.
Нулевая гипотеза в U-критерии Манна-Уитни всегда одна и та же, т. Е. Между двумя выборками нет значительной разницы.
Тест Манна-Уитни применяется к двум распределениям, которые не обязательно должны иметь нормальное распределение, но должны иметь одинаковую форму кривой. Например: если одна кривая (образца) имеет более длинный правый хвост, другая кривая (или другие образцы) также должна иметь более длинный правый хвост.

Преимущество использования U-критерия Манна-Уитни заключается в том, что он не оказывает никакого эффекта из-за выбросов, поскольку он учитывает медиану, а не среднее значение для теста.

Этапы выполнения теста Манна-Уитни U:

Соберите два образца: образец 1 и образец 2.
Возьмите первое наблюдение из выборки 1 и сравните его с наблюдениями в выборке 2. Подсчитайте количество наблюдений в выборке 2, которые меньше этого и равны ему. Например, 10 наблюдений в выборке 2 меньше, чем первое наблюдение в выборке 1, и 2 равны, тогда статистика U для этой выборки: 10 + 2 (1/2) = 11
Повторите шаг 2 для всех наблюдений в образце 1.
Сложите все ваши итоги, полученные на шагах 2 и 3. Это наша сумма рангов.
Теперь мы вычисляем статистику U по следующей формуле

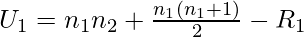
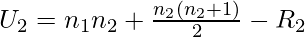
где:
- n ₁ : количество образцов в образце 1
- n ₂ : количество образцов в образце 2
- R ₁ : Сумма рангов образца 1
- R ₂ : Сумма рангов образца 2
Теперь наша тестовая статистика (U) будет меньше U ₁ и U ₂ .
Теперь посмотрим на критические значения в таблице относительно n ₁ и n ₂ (возьмем U ₀ ).
- если U <= U ₀ : мы отвергаем нулевую гипотезу.
- иначе мы не отвергаем нулевую гипотезу.

Примеры:

Предположим, что тест проводится на двух группах студентов, и его результаты приведены ниже:

Партия 1	Партия 2
3	9
4	7
2	5
6	10
2	8
5	6

Здесь наша нулевая гипотеза будет
- H ₀ : Нет существенной разницы между партиями.
- H _A : Между партиями существует значительная разница.
Здесь наш уровень значимости 0,05
Теперь мы ранжируем образцы по партиям, если две выборки имеют одинаковый ранг, мы будем усреднять ранг.

Партия 1	Ранг (партия 1)	Партия 2	Ранг (партия 2)
2	1.5	5	5.5
2	1.5	6	7,5
3	3	7	9
4	4	8	10
5	5.5	9	11
6	7,5	10	12
Сумма ранга	23	Сумма ранга	55

Теперь рассчитаем U-статистику:

[Текс] U_2 = 6 * 6 + 6 * 7/2 -55 = 2 [/ текс]

Итак, наша тестовая статистика U = min (U ₁ , U ₂ ) = min (34,2) = 2.
Теперь посмотрим на таблицу U-статистики для n ₁ = 6 и n ₂ = 6 и уровень значимости для таблицы ниже. Здесь наша критическая ценность:

Двусторонний тест Манна-Уитни

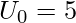
Здесь U <U ₀ , тогда мы отвергаем нулевую гипотезу.

Выполнение:

 # code for Mann-Whitney U test
 from scipy.stats import mannwhitneyu
 # Take batch 1 and batch 2 data as per above example
 batch_1 = [ 3 , 4 , 2 , 6 , 2 , 5 ]
 batch_2 = [ 9 , 7 , 5 , 10 , 8 , 6 ]
 
# perform mann whitney test
 stat, p_value = mannwhitneyu(batch_1, batch_2)
 print ( 'Statistics=%.2f, p=%.2f' % (stat, p_value))
 # Level of significance
 alpha = 0.05
 # conclusion
 if p_value < alpha:
    print ( 'Reject Null Hypothesis (Significant difference between two samples)' )
 else :
    print ( 'Do not Reject Null Hypothesis (No significant difference between two samples)' ) 

Выход:

 Статистика = 2,00, p = 0,01
Отклонить нулевую гипотезу (значительная разница между двумя образцами)

Машинное обучение

U-тест Манна и Уитни

РЕКОМЕНДУЕМЫЕ СТАТЬИ