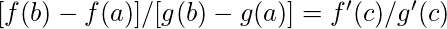Теорема Коши о среднем значении

Предположим, что f (x) и g (x) - две функции, удовлетворяющие трем условиям:

1) f (x), g (x) непрерывны на отрезке a <= x <= b

2) f (x), g (x) дифференцируемы на открытом интервале a <x <b и

3) g '(x)! = 0 для всех x принадлежит открытому интервалу a <x <b

Тогда согласно теореме Коши о среднем значении существует точка c в открытом интервале a <c <b такая, что:

Условия (1) и (2) точно такие же, как первые два условия теоремы Лагранжа о среднем значении для функций по отдельности. Теорема Лагранжа о среднем значении определена для одной функции, но она определена для двух функций.