Сумматоры и вычитатели в цифровой логике

Блок-схема комбинационной логической схемы:

Что следует помнить о комбинационной логической схеме:

1. Выход зависит от комбинации входов.
2. Выход - это чистая функция только текущих входов, т.е. входные данные предыдущего состояния не будут иметь никакого влияния на выход. Кроме того, он не использует память.
3. Другими словами,

    ВЫХОД = f (ВВОД)

4. Входы называются возбуждением от цепей, а выходы - откликом комбинационных логических цепей.

Классификация комбинационных логических схем:

1. Арифметика:

• Сумматоры
• Вычитатели
• Множители
• Компараторы

2. Обработка данных:

• Мультиплексоры
• Демультиплексоры
• Кодеры и декодеры

3. Преобразователи кода:

• BCD в код Excess-3 и наоборот
• BCD в код Грея и наоборот
• Семь сегментов

Дизайн полусумматоров и полных сумматоров:

• Схема комбинационной логики, которая выполняет сложение двух отдельных битов, называется полусумматором.
• Схема комбинационной логики, которая выполняет сложение трех отдельных битов, называется полным сумматором.

1. Полусумматор:

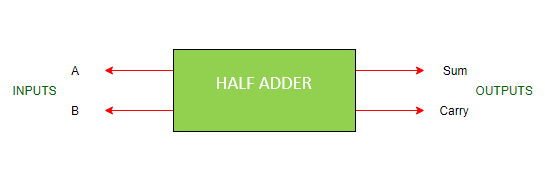
• Это арифметическая комбинационная логическая схема, предназначенная для сложения двух отдельных битов.
• Он содержит два входа и производит два выхода.
• Входы называются дополнительными и добавленными битами, а выходы - суммой и переносом.

Давайте посмотрим, как добавляются отдельные биты ,

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10

Поскольку 1 + 1 = 10, результат должен быть двухбитным. Итак, выше можно переписать как,

0 + 0 = 00
0 + 1 = 01
1 + 0 = 01
1 + 1 = 10

Результатом 1 + 1 является 10, где «1» - это выход с переносом (C _out ), а «0» - это суммарный выход (нормальный выход).

Таблица истинности полусумматора:

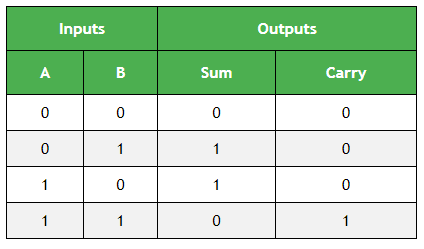
Следующим шагом будет построение логической диаграммы. Чтобы нарисовать логическую диаграмму, нам понадобится логическое выражение, которое можно получить с помощью K-карты (карта Карно). Поскольку есть две выходные переменные «S» и «C», нам нужно определить K-карту для каждой выходной переменной.

K-карта для выходной переменной Sum 'S':

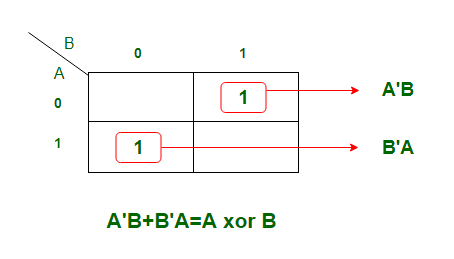
K-карта имеет форму суммы произведений. Полученное уравнение

 S = AB '+ A'B

что можно логически записать как,

 S = A xor B

K-карта для выходной переменной Carry 'C':

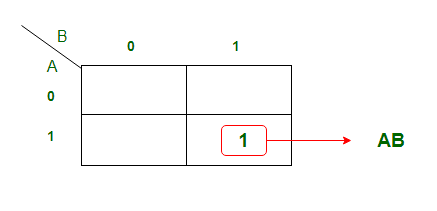
Уравнение, полученное из K-карты:

 C = AB

Используя логическое выражение, мы можем нарисовать логическую диаграмму следующим образом:

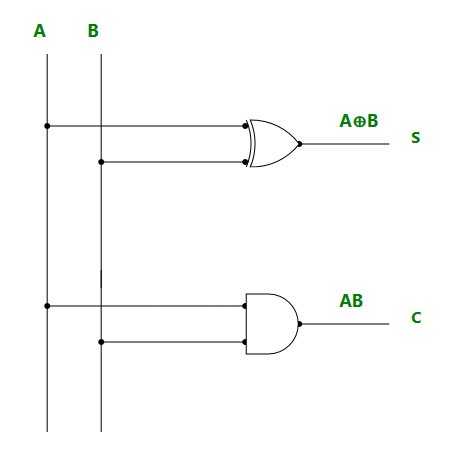
Ограничения:
Добавление переноса невозможно в Half Adder.

2. Полный сумматор:

• Чтобы преодолеть указанное выше ограничение, с которым сталкиваются полусумматоры, реализованы полные сумматоры.
• Это арифметическая комбинационная логическая схема, которая выполняет сложение трех отдельных битов.
• Он содержит три входа (A, B, C _in ) и производит два выхода (Sum и C _out ).
• Где, C _in -> Carry In и C _out -> Carry Out

Таблица истинности полного сумматора:

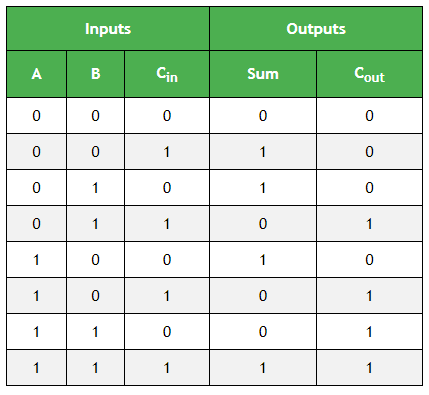
K-карта Упрощение для выходной переменной Sum 'S':

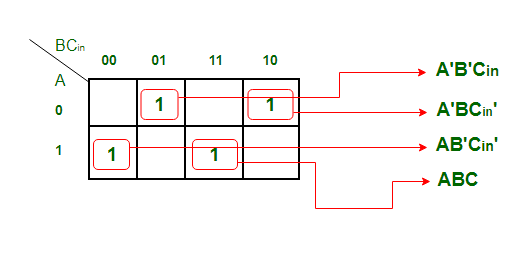
Полученное уравнение:

 S = A'B'C в + AB'C в '+ ABC + A'BC в '

Уравнение можно упростить как,

 S = B '(A'C in + AC in ') + B (AC + A'C in ')
S = B '(A xor C in ) + B (A xor C in )'
S = A xor B xor C в

K-карта Упрощение для выходной переменной 'C _out '

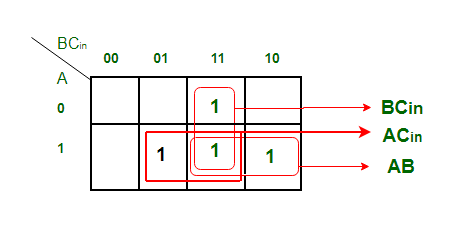
Полученное уравнение:

 C вне = BC в + AB + AC в

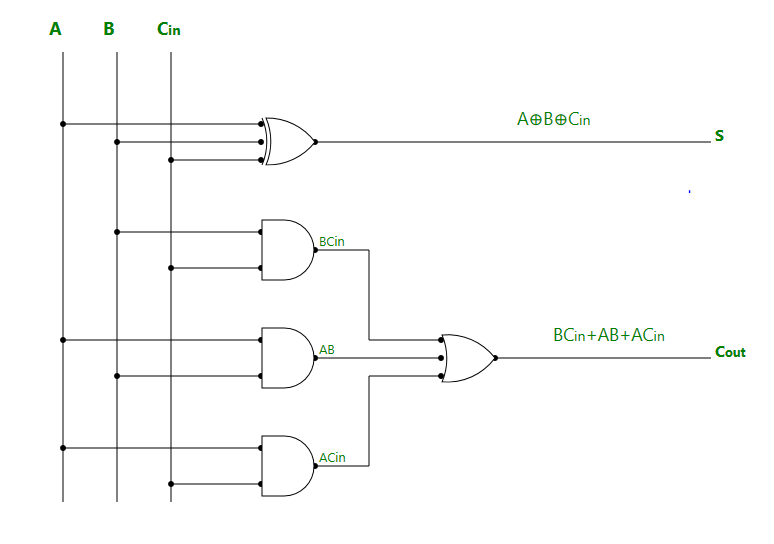
Логическая схема полного сумматора:

3. Половинный вычитатель:

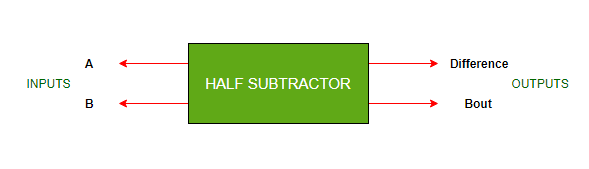
• Это комбинационная логическая схема, предназначенная для вычитания двух отдельных битов.
• Он содержит два входа (A и B) и производит два выхода (разность и заимствование-вывод).

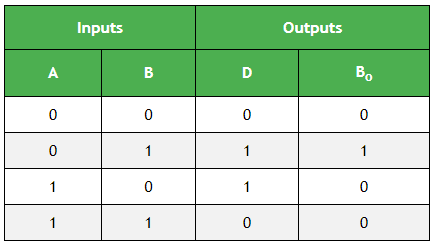
Таблица истинности полувычитателя:

K-карта Упрощение для выходной переменной 'D':

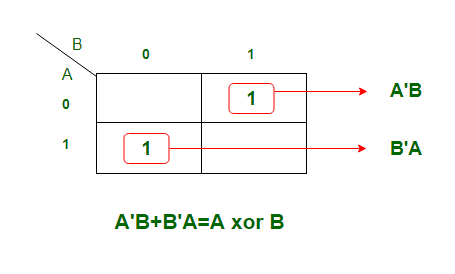
Полученное уравнение:

 D = A'B + AB '

что можно логически записать как,

 D = A xor B

K-карта Упрощение для выходной переменной 'B _out ':

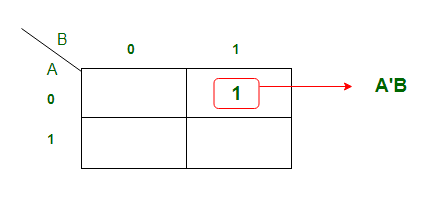
Уравнение, полученное из приведенной выше K-карты:

 B out = A'B

Логическая схема полувычитателя:

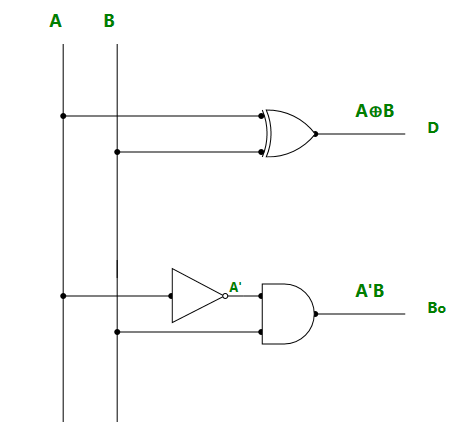
4. Полный вычитатель:

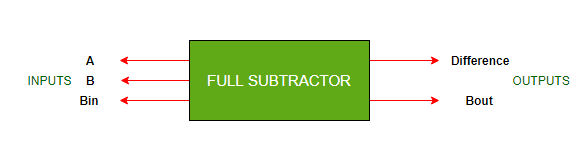
• Это комбинационная логическая схема, предназначенная для вычитания трех отдельных битов.
• Он содержит три входа (A, B, B _in ) и производит два выхода (D, B _out ).
• Где, A и B называются Minuend и Subtrahend битами.
• А, В _в -> Борроу-В и В _из -> Борроу-Out

Таблица истинности полного вычитателя:

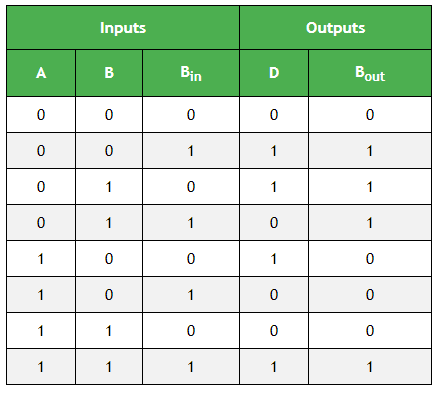
K-карта Упрощение для выходной переменной 'D':

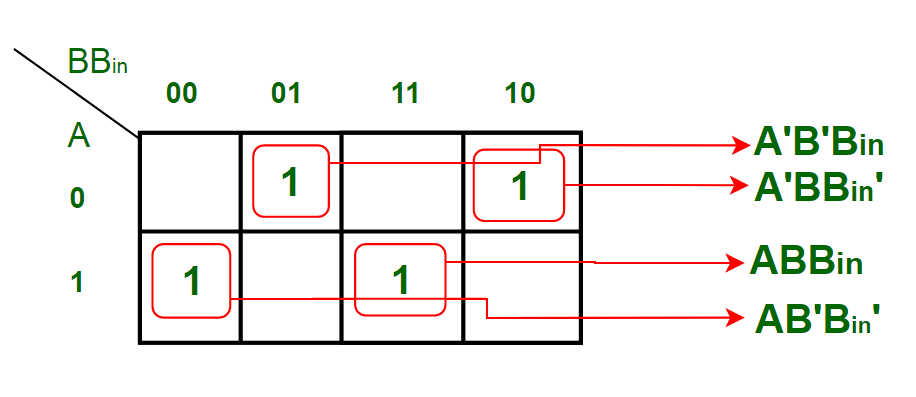
Уравнение, полученное из приведенной выше K-карты:

 D = A'B'B в + AB'B в '+ ABB в + A'BB в '

который можно упростить как,

 D = B '(A'B в + AB в ') + B (AB в + A'B в ')
D = B '(A xor B in ) + B (A xor B in )'
D = A xor B xor B в

K-карта Упрощение для выходной переменной 'B _out ':

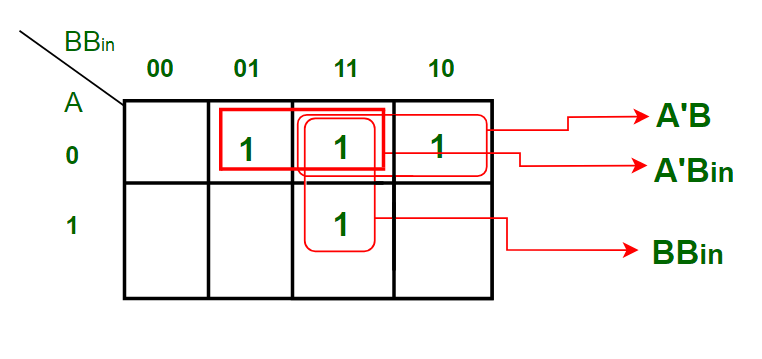
Полученное уравнение:

 Б из = BB + в A'B + A'B в

Логическая схема полного вычитателя:

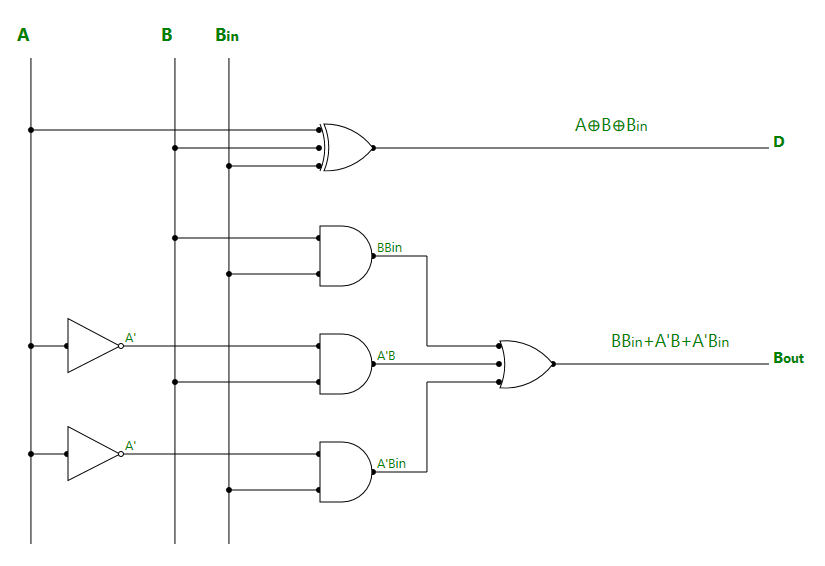
Приложения:

1. Для выполнения арифметических вычислений в электронных калькуляторах и других цифровых устройствах.
2. В таймерах и программных счетчиках.
3. Полезно при цифровой обработке сигналов.