Самая длинная палиндромная подстрока с использованием динамического программирования

Дана строка, найдите самую длинную подстроку, которая является палиндромом.

Пример:

Input: Given string :”forgeeksskeegfor”, 
Output: “geeksskeeg”

Input: Given string :”Geeks”, 
Output: “ee”

Способ 1 : грубая сила.
Подход: простой подход заключается в проверке каждой подстроки, является ли подстрока палиндромом или нет. Для этого сначала запустите три вложенных цикла, два внешних цикла выбирают все подстроки одну за другой, фиксируя угловые символы, внутренний цикл проверяет, является ли выбранная подстрока палиндромом или нет.

Ниже приведена реализация вышеуказанного подхода:

Анализ сложности:

• Временная сложность: O(n^3).
  Чтобы найти самую длинную палиндромную подстроку в этом подходе, необходимы три вложенных цикла, поэтому временная сложность составляет O (n ^ 3).
• Вспомогательная сложность : O(1).
  Так как не нужно дополнительное место.

Метод 2 : динамическое программирование.
Подход: временная сложность может быть уменьшена за счет сохранения результатов подзадач.

1. Поддерживайте логическую таблицу [n][n], которая заполняется снизу вверх.
2. Значение table[i][j] равно true, если подстрока является палиндромом, иначе false.
3. Чтобы вычислить table[i][j], проверьте значение table[i+1][j-1], если значение истинно, а str[i] такое же, как str[j], тогда мы делаем table[i ][j] верно.
4. В противном случае значение table[i][j] становится ложным.
5. Мы должны заполнить таблицу ранее для подстроки длины = 1 и длины = 2, потому что
   как мы находим, если table[i+1][j-1] является истинным или ложным, поэтому в случае
   (i) length == 1 , скажем, i=2 , j=2 и i+1,j-1 не лежит между [i , j]
   (ii) length == 2, скажем, i=2, j=3 и i+1,j-1 снова не лежит между [i, j].

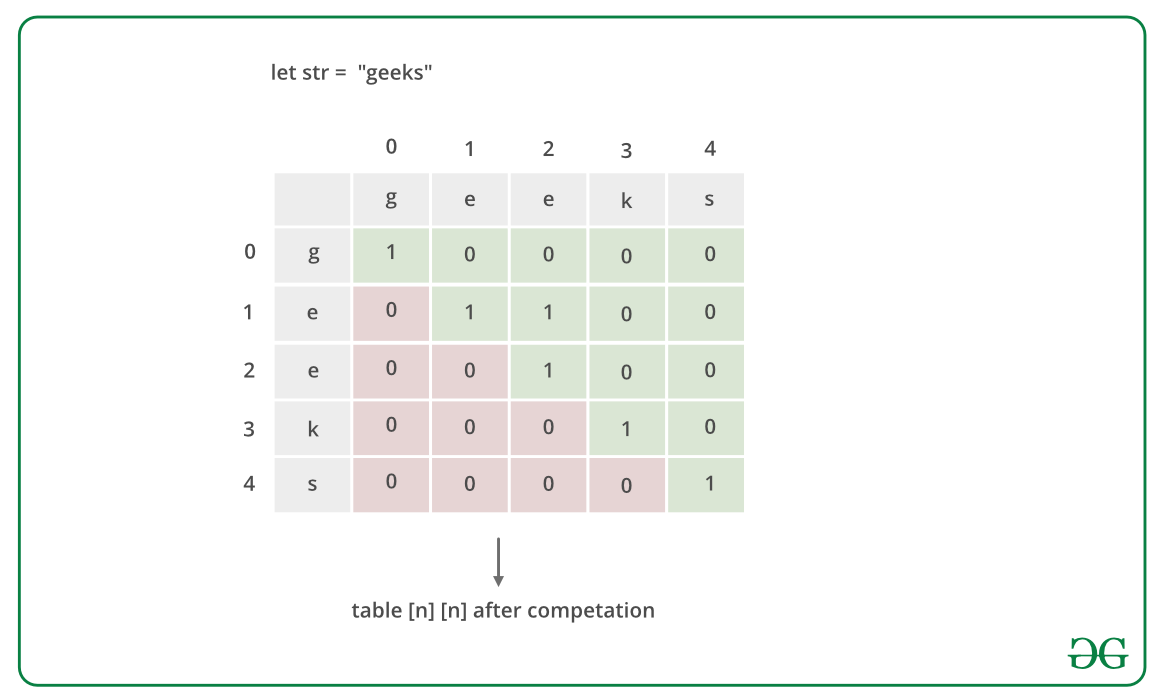
Ниже приведена реализация вышеуказанного подхода:

Анализ сложности:

• Временная сложность : O(n^2).
  Нужны два вложенных обхода.
• Вспомогательное пространство : O(n^2).
  Матрица размера n*n необходима для хранения массива dp.