Самая большая прямоугольная область на гистограмме с использованием стека

Найдите наибольшую возможную прямоугольную область на данной гистограмме, где самый большой прямоугольник может быть составлен из ряда смежных столбцов, высоты которых заданы в виде массива. Для простоты предположим, что все столбцы имеют одинаковую ширину, а ширина равна 1 единице.

Пример:

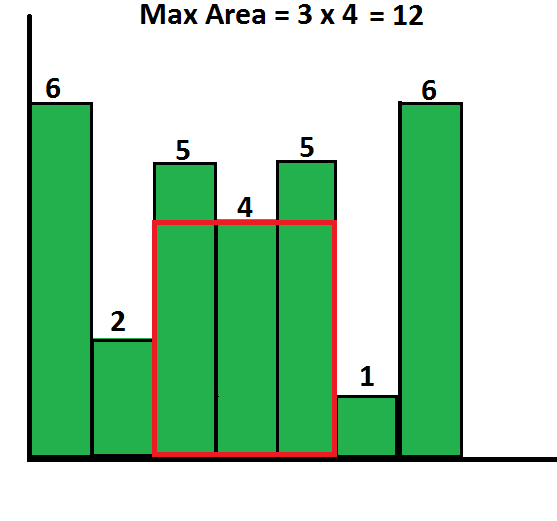
Input: histogram = {6, 2, 5, 4, 5, 1, 6}
 

Output: 12

Input: histogram = {3, 5, 1, 7, 5, 9}
Output: 15

Чтобы решить проблему, следуйте следующей идее:

For every bar ‘x’, we calculate the area with ‘x’ as the smallest bar in the rectangle. If we calculate the such area for every bar ‘x’ and find the maximum of all areas, our task is done. 

How to calculate the area with ‘x’ as the smallest bar? 

We need to know the index of the first smaller (smaller than ‘x’) bar on the left of ‘x’ and the index of the first smaller bar on the right of ‘x’. Let us call these indexes as ‘left index’ and ‘right index’ respectively. We traverse all bars from left to right and maintain a stack of bars. Every bar is pushed to stack once. A bar is popped from the stack when a bar of smaller height is seen. When a bar is popped, we calculate the area with the popped bar as the smallest bar. 

How do we get the left and right indexes of the popped bar?

The current index tells us the right index and the index of the previous item in the stack is the left index

Выполните указанные шаги, чтобы решить проблему:

1. Создайте пустой стек.
2. Начните с первого бара и выполните следующие действия для каждого бара hist[i], где ' i ' варьируется от 0 до n-1.
   1. Если стек пуст или hist[i] выше, чем полоса наверху стека, нажмите ' i ', чтобы сложить.
   2. Если этот брусок меньше вершины стека, то продолжайте удалять вершину стека, пока вершина стека больше.
   3. Пусть удаленный бар будет hist[tp]. Вычислите площадь прямоугольника с hist[tp] в качестве наименьшего бара.
   4. Для hist[tp] «левый индекс» — это предыдущий (предшествующий tp) элемент в стеке, а «правый индекс» — это « i » (текущий индекс).
3. Если стек не пуст, то по одному удаляем из стека все бары и делаем шаг (2.2 и 2.3) для каждого удаленного бара

Ниже приведена реализация описанного выше подхода.

Временная сложность: O(N), так как каждый бар толкается и выталкивается только один раз
Вспомогательное пространство: O(N)

Наибольшая прямоугольная площадь в гистограмме путем нахождения следующего и предыдущего меньшего элемента:

Чтобы решить проблему, следуйте следующей идее:

Find the previous and the next smaller element for every element of the histogram, as this would help to calculate the length of the subarray in which this current element is the minimum element. So we can create a rectangle of size (current element * length of the subarray) using this element. Take the maximum of all such rectangles.

Выполните указанные шаги, чтобы решить проблему:

• Во-первых, мы возьмем два массива left_smaller[] и right_smaller[] и инициализируем их значениями -1 и n соответственно.
• Для каждого элемента мы будем хранить индекс предыдущего меньшего и следующего меньшего элемента в массивах left_smaller[] и right_smaller[] соответственно.
• Теперь для каждого элемента мы вычислим площадь, взяв этот i- ^й элемент как наименьший в диапазоне left_smaller[i] и right_smaller[i] и умножив его на разницу между left_smaller[i] и right_smaller[i]
• Мы можем найти максимум всех площадей, рассчитанных на шаге 3, чтобы получить желаемую максимальную площадь.

Ниже приведена реализация описанного выше подхода.

Временная сложность: O(N)
Вспомогательное пространство: O(N)

Похожие статьи: Разделяй и властвуй на основе решения O(N log N)

Спасибо Ашишу Ананду за предложение первоначального решения. Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.