Регуляризация в машинном обучении
Предварительные требования: градиентный спуск
Переобучение - это явление, которое возникает, когда модель машинного обучения ограничена обучающим набором и не может хорошо работать с невидимыми данными.
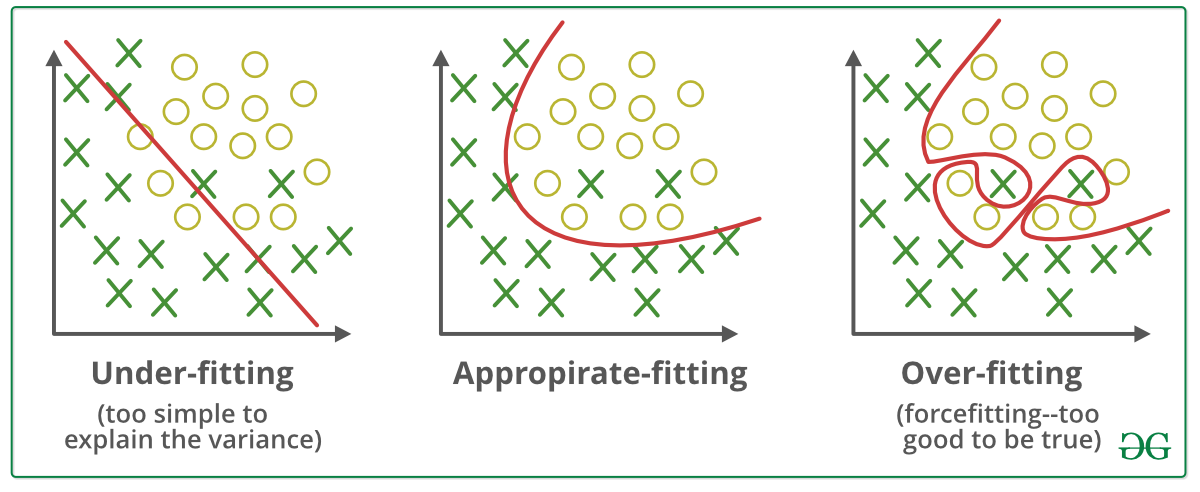
Регуляризация - это метод, используемый для уменьшения ошибок путем подходящей подгонки функции к данному обучающему набору и предотвращения переобучения.
Обычно используются следующие методы регуляризации:
- L1 регуляризация
- L2 регуляризация
- Регуляризация отсева
Эта статья посвящена регуляризации L1 и L2.
Модель регрессии, в которой используется метод регуляризации L1 , называется регрессией LASSO (оператор наименьшего абсолютного сжатия и выбора) .
Модель регрессии, использующая метод регуляризации L2 , называется регрессией Риджа .
Регрессия Лассо добавляет «абсолютное значение величины» коэффициента в качестве штрафного члена к функции потерь (L).
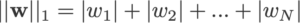
Регрессия Риджа добавляет « квадрат величины » коэффициента в качестве штрафного члена к функции потерь (L).

ЗАМЕТЬТЕ, что во время регуляризации функция вывода (y_hat) не изменяется. Изменение только в функции потерь.
Функция вывода:
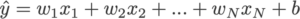
Функция потерь до регуляризации:

Функция потерь после регуляризации:
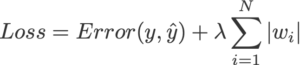
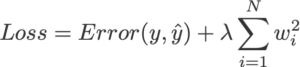
Мы определяем функцию потерь в логистической регрессии как:
L (y_hat, y) = y log y_hat + (1 - y) log (1 - y_hat)
Функция потерь без регуляризации:
L = y log (wx + b) + (1 - y) log (1 - (wx + b))
Допустим, данные превышают указанную выше функцию.
Функция потерь с регуляризацией L1:
L = y log (wx + b) + (1 - y) log (1 - (wx + b)) + лямбда * || w || 1
Функция потерь с регуляризацией L2:
L = y log (wx + b) + (1 - y) log (1 - (wx + b)) + лямбда * || w || 2 2
лямбда - это гиперпараметр, известный как константа регуляризации, и он больше нуля.
лямбда> 0