Разница между десятичной и двоичной системами счисления
В математике система, которая используется для представления чисел в различных формах, определяется как система счисления . Математическое значение, которое используется для подсчета, измерения и выполнения различных арифметических вычислений, называется числом. В зависимости от свойств числа подразделяются на различные типы, такие как натуральные числа, целые числа, дроби, рациональные и иррациональные числа и так далее. Точно так же у нас есть разные виды систем счисления, основанные на разных свойствах, такие как двоичная система счисления, восьмеричная система счисления, десятичная система счисления и шестнадцатеричная система счисления. Мы можем преобразовать число из любой системы счисления в любую из трех других систем счисления.
Десятичная система счисления
Система счисления, которая представляет число от 0 до 9 цифр, является десятичной системой счисления . Десятичная система счисления состоит из десяти цифр, т. е. 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Основание числа в этой системе равно 10. В десятичной системе счисления число выражается в терминах степеней 10, т. е. позиции последовательных цифр слева от десятичной точки представляют единицы, десятки, сотни, тысячи и т. д. Некоторые примеры чисел в десятичной системе счисления: (23) 10 , (123) 10 , (5547) 10 , (6531) 10 и так далее. В повседневной жизни мы чаще всего представляем числа в десятичной системе счисления.
Например, (123) 10 в степени 10 выражается как 1 × 10 2 + 2 × 10 1 + 3 × 10 0 . 1 в разряде сотен, 2 в разряде десятков и 3 в разряде единиц.
Двоичная система счисления
Система счисления, которая выражает число цифрами 0 и 1, называется двоичной системой счисления. Двоичная система имеет только две цифры, т. е. 0 и 1. Основание числа в этой системе равно 2. В двоичной системе счисления число выражается через степени двойки. Например, десятичное число 26 равно выражается как (11010) 2 в двоичной системе. Двоичные цифры 0 и 1 используются во всех компьютерных программах и языках, таких как C, C++, Java и т. д., для написания программы и кодирования любых цифровых данных.
Двоичное число (1011) 2 выражается в степени двойки как (1 × 2 3 ) + (0 × 2 2 ) + (1 × 2 1 ) + (1 × 2 0 ).
Десятичное число | Двоичный номер |
|---|---|
1 | 01 |
2 | 10 |
3 | 11 |
4 | 100 |
5 | 101 |
6 | 110 |
7 | 111 |
8 | 1000 |
9 | 1001 |
10 | 1010 |
Преобразование двоичного в десятичное и наоборот
Двоичные числа можно преобразовать в десятичные числа, а десятичные числа можно преобразовать обратно в двоичные числа, используя следующие правила:
Двоичное в десятичное преобразование
Система счисления, которая выражает число цифрами от 0 до 1, является двоичной системой счисления, тогда как десятичная система счисления представляет число цифрами от 0 до 9. Теперь, чтобы преобразовать двоичное число в десятичное, умножьте каждую цифру двоичного числа на степень 2.
Если B = a n-1 …a 3 a 2 a 1 a 0 — двоичное число, состоящее из n цифр, то соответствующее десятичное число будет
D = (a n-1 × 2 n-1 ) +…+(a 3 × 2 3 ) + (a 2 × 2 2 ) + (a 1 × 2 1 ) + (a 0 × 2 0 ).
Пример: Преобразуйте (11001) 2 в десятичное число.
Решение:
The given binary number is (11001)2.
(11001)2 = (1 × 24) + (1 × 23) + (0 × 22) + (0 × 21) + (1 × 20)
= 16 + 8 + 0 + 0 + 1 = (25)10
Therefore, the binary number (11001)2 is expressed as (25)10.
Десятичное в двоичное преобразование
Чтобы преобразовать десятичное число в двоичное, непрерывно делите данное число на 2, пока не получите частное, равное 1. Обратите внимание, что мы должны записывать числа снизу вверх.
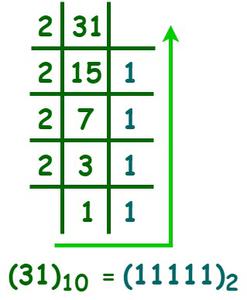
Пример: преобразовать (31) 10 в двоичное число.
Решение:
Therefore, (31)10 is expressed as (11111)2
Разница между двоичной и десятичной системами
Двоичная система счисления | Десятичная система счисления |
|---|---|
| Система счисления, которая выражает число цифрами 0 и 1, является двоичной системой счисления. | Система счисления, которая представляет число от 0 до 9 цифр, является десятичной системой счисления. |
| Двоичная система имеет только две цифры, то есть 0 и 1. | Десятичная система счисления состоит из десяти цифр, то есть 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. |
| Основание числа в этой системе равно 2. | Основание числа в этой системе равно 10. |
| В двоичной системе счисления число выражается в степени двойки. | В десятичной системе счисления число выражается в степени 10. |
| Десятичное число 26 выражается как (11010) 2 в двоичной системе. | Двоичное число (11010) 2 равно 26 в десятичной системе счисления. |
Решенный пример преобразования двоичного числа в десятичное и наоборот
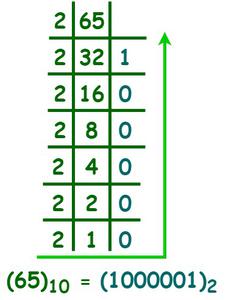
Пример 1: Преобразование (65) 10 в двоичное число.
Решение:
Therefore, (65)10 is expressed as (1000001)2
Пример 2. Преобразование (10101) 2 в десятичное число.
Решение:
The given binary number is (10101)2.
(10101)2 = (1 × 24) + (0 × 23) + (1 × 22) + (0 × 21) + (1 × 20)
= 16 + 0 + 4 + 0 + 1 = (21)10
Therefore, the binary number (10101)2 is expressed as (21)10.
Пример 3: Преобразование (111001) 2 в десятичное число.
Решение:
The given binary number is (111001)2.
(10101)2 = (1 × 25) + (1 × 24) + (1 × 23) + (0 × 22) + (0 × 21) + (1 × 20)
= 32 + 16 + 8 + 0 + 0 + 1 = (57)10
Therefore, the binary number (111001)2 is expressed as (57)10.
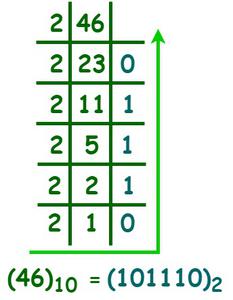
Пример 4: Преобразование (46) 10 в двоичное число.
Решение:
Therefore, (46)10 is expressed as (101110)2.
Часто задаваемые вопросы о десятичной и двоичной системе счисления
Вопрос 1: Что такое двоичная и десятичная системы счисления?
Отвечать:
The number system that expresses a number in terms of 0 and 1 digits is a binary number system, whereas a decimal number system represents a number in terms of 0 to 9 digits.
Вопрос 2: Как вы можете преобразовать двоичное число в десятичное число?
Отвечать:
To convert a binary number into a decimal number, multiply each digit of the binary number by the power of 2. If B = an-1…a3a2a1a0 is a binary number that has n digits, then the respective decimal number will be
D = (an-1 × 2n-1) +…+(a3 × 23) + (a2 × 22) + (a1 × 21) + (a0 × 20).
Вопрос 3: Как преобразовать десятичное число в двоичное?
Отвечать:
To convert a decimal number into a binary number, divide the given number by 2 continuously till we get the quotient as 1. Note that we have to write the numbers from downwards to upwards.
Вопрос 4: В чем разница между двоичной и десятичной системами счисления?
Отвечать:
The number system that expresses a number in terms of 0 and 1 digits is a binary number system, whereas a decimal number system represents a number in terms of 0 to 9 digits. In a binary number system, a number is expressed in terms of powers of 2, whereas in a decimal number system a number is expressed in terms of powers of 10.
Вопрос 5: Какое десятичное число эквивалентно двоичному числу 11010?
Отвечать:
11010 = (1 × 24) + (1 × 23) + (0 × 22) + (1 × 21) + (0 × 20)
= 16 + 8 + 0 + 2 + 0 = 26
So, (11010)2 is 26 in the decimal number system.