Реализовать быструю сортировку с первым элементом в качестве опорного

QuickSort — это алгоритм «разделяй и властвуй» . Он выбирает элемент в качестве опорного элемента и разбивает заданный массив вокруг опорного элемента. Существует много разных версий quickSort, которые по-разному выбирают опорную точку.

• Всегда выбирайте первый элемент в качестве опорного.
• Всегда выбирайте последний элемент в качестве опорного.
• Выберите случайный элемент в качестве точки опоры.
• Выберите медиану в качестве точки опоры.

Примечание. Здесь мы реализуем быструю сортировку, выбрав первый элемент в качестве опорного.

Быстрая сортировка путем выбора первого элемента в качестве опорного.

Ключевой функцией быстрой сортировки является разделение. Цель разделов состоит в том, чтобы поместить стержень в правильное положение, если массив отсортирован и меньшие (или равные) элементы слева, а более высокие элементы справа, и сделать все это за линейное время .

Алгоритм разделения:

Существует множество способов разбиения, следующий псевдокод использует метод, описанный в книге CLRS.

• Мы начинаем с самого левого элемента и отслеживаем индекс меньших (или равных) элементов как i .
• При обходе, если мы находим меньший (или равный) элемент, мы меняем текущий элемент на arr[i].
• В противном случае мы игнорируем текущий элемент.

Псевдокод для рекурсивной функции QuickSort:

// low  –> Starting index,  high  –> Ending index

quickSort(arr[], low, high) {
    if (low < high) {
        
        // pi is partitioning index, arr[pi] is now at right place
        pi = partition(arr, low, high);
        quickSort(arr, low, pi – 1);  // Before pi
        quickSort(arr, pi + 1, high); // After pi
    }
}

Псевдокод для функции partition()

/* This function takes first element as pivot, places the pivot element at its correct position in sorted array, and places all smaller (smaller than or equal to pivot) to left of pivot and all greater elements to right of pivot */

partition (arr[], low, high) {
    // first element as pivot
    pivot = arr[low]
    k = high
    for (i = high; i > low; i–) {
        if (arr[i] > pivot){
            swap arr[i] and arr[k];
            k–;
        }
    }
    swap arr[k] and arr[low]
    return k-1;
}

Иллюстрация раздела () :

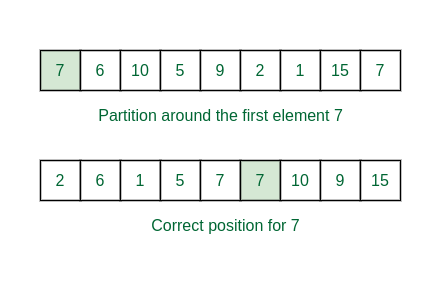
Consider: arr[] = { 7,   6,   10,   5,   9,   2,   1,   15,   7 }

First Partition: low = 0, high = 8, pivot = arr[low] = 7
Initialize index of right most element k = high = 8.

• Traverse from i = high to low:
  • if arr[i] is greater than pivot:
    • Swap arr[i] and arr[k].
    • Decrement k;
• At the end swap arr[low] and arr[k].

Now the correct position of pivot is index 5

First partition

Second Partition: low = 0, high = 4, pivot = arr[low] = 2
Similarly initialize k = high = 4; 

The correct position of 2 becomes index 1. And the left part is only one element and the right part has {6, 5, 7}.

Partition of the left half

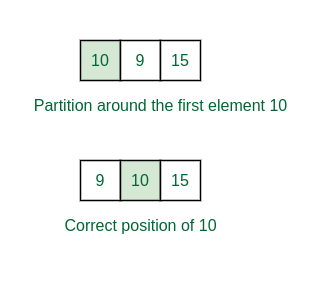
On the other hand partition happens on the segment [6, 8] i.e., the array {10, 9, 15}.
Here low = 6, high = 8, pivot = 10 and k = 8.

The correct position of 10 becomes index 7 and the right and left part both has only one element.

Partition of the right half

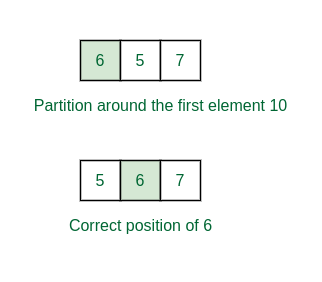
Third partition:  Here partition the segment {6, 5, 7}. The low = 2, high = 4, pivot = 6 and k = 4.
If the same process is applied, we get correct position of 6 as index 3 and the left and the right part is having only one element.

Third partition

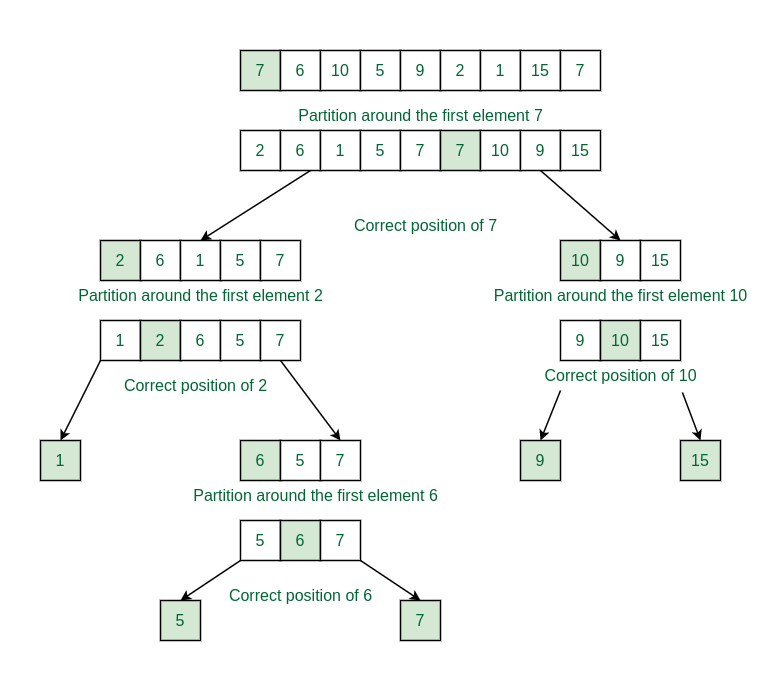
The total array becomes sorted in this way. Check the below image for the recursion tree

Recursion tree for partitions

Выполните следующие шаги, чтобы реализовать подход.

• Используйте рекурсивную функцию (скажем, quickSort ) для инициализации функции.
• Вызовите функцию разделения, чтобы разбить массив, и внутри функции разделения выполните следующие действия.
  • Возьмите первый элемент в качестве опорного и инициализируйте его, а итератор k = high .
  • Итерация в цикле for от i = high до low+1:
    • Если arr[i] больше, чем pivot, то поменяйте местами arr[i] и arr[k] и уменьшите k.
  • После итерации поменяйте ось на arr[k] .
  • Верните k-1 как точку раздела.
• Теперь рекурсивно вызовите quickSort для левой и правой половины индекса раздела.

Реализация вышеуказанного подхода.

Анализ сложности:

• Сложность времени:
  • Средний случай : O(N * logN), где N — длина массива.
  • Лучший случай: O(N * logN)
  • Худший случай: O(N ² )
• Вспомогательное пространство: O(1)