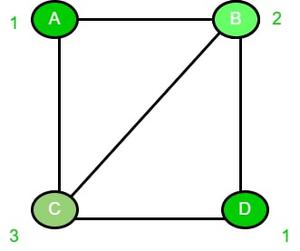
Раскраска хордальных графов

В математической теории графов хордовый граф представляет собой замкнутый контур, имеющий 4 или более вершин, так что ребро можно провести из одной вершины в другую вершину, присутствующую в нем. Другими словами, хордовый граф — это граф длины 4 или более, содержащий хотя бы одну хорду. Хорда — это не что иное, как ребро, соединяющее две вершины графа и проведенное внутри графа.

Важные моменты, которые следует помнить:

• Хордальный граф — это подмножество полного графа.
• Граф, не содержащий хорды, называется дырочным или бесхордовым циклом.
• Полный граф сам по себе хордовый граф.

1) Рассмотрим приведенный ниже граф ABCD c. Ребро CB проведено из вершины C в вершину B, которая действует как хорда в этом графе. Следовательно, приведенный ниже граф называется хордовым графом.

2) Рассмотрим приведенный ниже пример полного графа. Граф, состоящий из n*(n-1)/2 ребер, называется полным графом, где n — количество вершин. В полном графе ребра, соединяющие все вершины, уже присутствуют и также действуют как хорда. Следовательно, полный граф является надмножеством хордового графа.

Алгоритм минимальной окраски:

В этой статье мы обсудим раскраску хордовых графов с помощью жадного алгоритма раскраски.

Алгоритм жадной раскраски:

1. Во-первых, нам нужно найти идеальный порядок исключения (PEO) данного хордового графа.
2. Затем проходим вершины в порядке, обратном тому ПЭО, который мы уже нашли.
3. Придает наименьший цвет каждой вершине, чтобы текущий цвет вершины не использовался в соседних вершинах.
4. Если цвет текущей вершины уже задан ее соседу, увеличьте цвет и назначьте его текущей вершине.
5. Повторяйте шаги 3 и 4, пока все вершины не будут окрашены.

Пример. Рассмотрим приведенный ниже хордальный граф ABCD. Пусть идеальный порядок исключения этого графа будет [D, C, B, A]. Мы пройдем по графу PEO в обратном направлении. Следовательно, [A, B, C, D] является обратным PEO.

1. Во-первых, мы раскрасим вершину A в 1, так как нам нужно покрасить ее в наименьший существующий цвет.

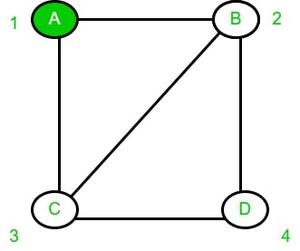
2. Теперь для вершины B проверим, содержат ли ее соседи цвет 1 или нет. Поскольку вершина «А» содержит цвет 1, поэтому мы увеличим цвет на 1, чтобы покрасить вершину В.

3. Точно так же для вершины C ее соседка A содержит цвет 1, а B содержит цвет 2, поэтому мы окрасим вершину C в 3.

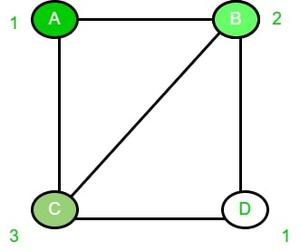
4. Теперь для вершины D, поскольку ее соседи не содержат цвета 1, мы окрасим 1 в вершину D.