r-Ближайшие соседи

Опубликовано: 23 Июля, 2021

r-Ближайшие соседи - это модифицированная версия k-ближайших соседей. Проблема с k-ближайшими соседями заключается в выборе k. Чем меньше k, тем выше чувствительность классификатора к выбросам. Если значение k велико, тогда классификатор будет включать много точек из других классов. Именно из этой логики мы получаем алгоритм r ближайших соседей.

Интуиция:
Рассмотрим следующие данные в качестве обучающей выборки.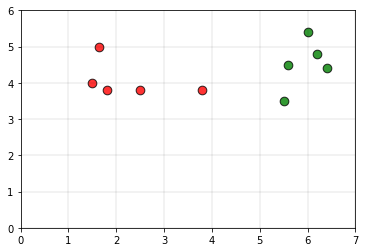

Точки зеленого цвета относятся к классу 0, а точки красного цвета относятся к классу 1.
Рассмотрим белую точку P как точку запроса, чья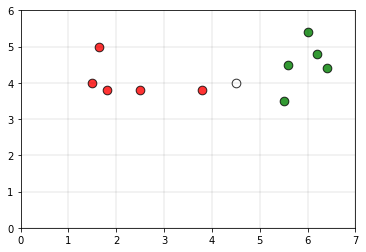

Если мы возьмем радиус круга равным 2,2 единицы, и если круг будет нарисован с использованием точки P в качестве центра круга, график будет следующим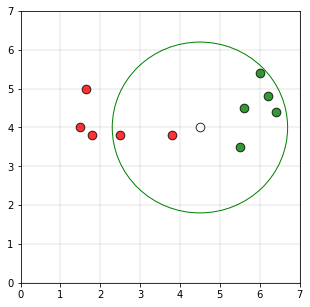

Поскольку количество точек в круге, принадлежащих к классу 1 (5 баллов) больше, чем количество точек, принадлежащих к классу 0 (2 балла)

Алгоритм:

Step 1: Given the point P, determine the sub-set of data that lies in the ball of radius r centered at P,
B_r (P) = { X_i ∊ X | dist( P, X_i ) ≤ r }
Step 2: If B_r (P) is empty, then output the majority class of the entire data set.
Step 3: If B_r (P) is not empty, output the majority class of the data points in it.

Реализация алгоритма соседей с радиусом r выглядит следующим образом:

C / C ++

 // C++ program to implement the
 // r nearest neighbours algorithm.
 #include <bits/stdc++.h>
 using namespace std;
 
struct Point
 {
    // Class of point
    int val;
     
    // Co-ordinate of point
    double x, y;
 };
 
// This function classifies the point p using
 // rk neareast neighbour algorithm. It assumes only
 // two groups and returns 0 if p belongs to class 0, else
 // 1 (belongs to class 1).
 int rNN(Point arr[], int n, float r, Point p)
 {
    // frequency of group 0
    int freq1 = 0;
    // frequency of group 1
    int freq2 = 0;
 
    // Check if the distance is less than r
    for ( int i = 0; i < n; i++)
    {
 
        if (( sqrt ((arr[i].x - px) * (arr[i].x - px) +
        (arr[i].y - py) * (arr[i].y - py))) <= r)
        {
            if (arr[i].val == 0)
                freq1++;
            else if (arr[i].val == 1)
                freq2++;
        }
    }
    return (freq1 > freq2 ? 0 : 1);
 }
 
// Driver code
 int main()
 {
    // Number of data points
    int n = 10;
    Point arr[n];
 
    arr[0].x = 1.5;
    arr[0].y = 4;
    arr[0].val = 0;
 
    arr[1].x = 1.8;
    arr[1].y = 3.8;
    arr[1].val = 0;
 
    arr[2].x = 1.65;
    arr[2].y = 5;
    arr[2].val = 0;
 
    arr[3].x = 2.5;
    arr[3].y = 3.8;
    arr[3].val = 0;
 
    arr[4].x = 3.8;
    arr[4].y = 3.8;
    arr[4].val = 0;
 
    arr[5].x = 5.5;
    arr[5].y = 3.5;
    arr[5].val = 1;
 
    arr[6].x = 5.6;
    arr[6].y = 4.5;
    arr[6].val = 1;
 
    arr[7].x = 6;
    arr[7].y = 5.4;
    arr[7].val = 1;
 
    arr[8].x = 6.2;
    arr[8].y = 4.8;
    arr[8].val = 1;
 
    arr[9].x = 6.4;
    arr[9].y = 4.4;
    arr[9].val = 1;
 
    // Query point
    Point p;
    px = 4.5;
    py = 4;
 
    // Parameter to decide the class of the query point
    float r = 2.2;
    printf ( "The value classified to query point"
           " is: %d.
" , rNN(arr, n, r, p));
    return 0;
 }

Python3

 # Python3 program to implement the
 # r nearest neighbours algorithm.
 import math
 
def rNN(points, p, r = 2.2 ):
        '''
        This function classifies the point p using
        rk neareast neighbour algorithm. It assumes only
        two groups and returns 0 if p belongs to class 0, else
        1 (belongs to class 1).
 
        Parameters -
                points : Dictionary of training points having two
                         keys - 0 and 1. Each class have a list of
                         training data points belonging to them
 
                p : A tuple, test data point of form (x, y)
                k : radius of the r nearest neighbors
        '''
 
        freq1 = 0
        freq2 = 0
        for group in points:
                for feature in points[group]:
                        if math.sqrt((feature[ 0 ] - p[ 0 ]) * * 2 +
                                     (feature[ 1 ] - p[ 1 ]) * * 2 ) < = r:
                                if group = = 0 :
                                        freq1 + = 1
                                group elif = = 1 :
                                        freq2 + = 1
                         
        return 0 if freq1>freq2 else 1
 
# Driver function
 def main():
 
        # Dictionary of training points having two keys - 0 and 1
        # key 0 have points belong to class 0
        # key 1 have points belong to class 1
 
        points = { 0 :[( 1.5 , 4 ), ( 1.8 , 3.8 ), ( 1.65 , 5 ), ( 2.5 , 3.8 ), ( 3.8 , 3.8 )],
                  1 :[( 5.5 , 3.5 ), ( 5.6 , 4.5 ), ( 6 , 5.4 ), ( 6.2 , 4.8 ), ( 6.4 , 4.4 )]}
 
        # query point p(x, y)
        p = ( 4.5 , 4 )
 
        # Parameter to decide the class of the query point
        r = 2.2
 
        print ( "The value classified to query point is: {}" . format (
                rNN(points, p, r)))
 
if __name__ = = '__main__' :
        main()

Выход:

Значение, отнесенное к точке запроса: 1.

Другие методы, такие как kd-tree, хеширование с учетом местоположения, могут использоваться для уменьшения временной сложности поиска соседей.

Приложения:
Этот алгоритм можно использовать для выявления выбросов. Если узор не имеет никакого сходства с узорами в пределах выбранного радиуса, он может быть идентифицирован как выброс.

Внимание компьютерщик! Укрепите свои основы с помощью базового курса программирования Python и изучите основы.

Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS. А чтобы начать свое путешествие по машинному обучению, присоединяйтесь к курсу Машинное обучение - базовый уровень.

Python Машинное обучение C++ Продвинутая компьютерная тематика

r-Ближайшие соседи

C / C ++

Python3

РЕКОМЕНДУЕМЫЕ СТАТЬИ