Python - тест хи-квадрат Пирсона
Статистическая гипотеза хи-квадрат Пирсона - это проверка независимости категориальных переменных. В этой статье мы проведем тест с использованием математического подхода, а затем с использованием модуля Python SciPy.
Во-первых, давайте посмотрим на математический подход:
Таблица непредвиденных обстоятельств:
Таблица непредвиденных обстоятельств (также называемая кросс-таблицей) используется в статистике для обобщения взаимосвязей между несколькими категориальными переменными. Здесь мы возьмем таблицу, которая показывает количество мужчин и женщин, покупающих разные виды домашних животных. собака Кот птица общее люди 207 282 241 730 женщины 234 242 232 708 общее 441 524 473 1438
Цель теста - определить, связаны ли две переменные (пол и выбор домашнего животного) друг с другом.
Нулевая гипотеза:
Мы начинаем с определения нулевой гипотезы ( H0 ), которая утверждает, что нет никакой связи между переменными. Альтернативная гипотеза могла бы утверждать, что между ними существует значительная связь .
Мы можем проверить гипотезу следующими методами:
- Используя p-значение :
Мы определяем фактор значимости, чтобы определить, имеет ли отношение между переменными значимость. Обычно выбирается коэффициент значимости или значение альфа 0,05. Это альфа-значение обозначает вероятность ошибочного отклонения H0, когда оно истинно. Меньшее значение альфа выбирается в тех случаях, когда мы ожидаем большей точности. Если значение p для теста оказывается строго больше, чем значение альфа, то H0 остается верным.
- Используя значение хи-квадрат :
Если рассчитанное нами значение хи-квадрат меньше или равно табличному (также называемому критическим ) значению хи-квадрат, то H0 остается верным.
Таблица ожидаемых значений:
Далее готовим аналогичную таблицу расчетных (или ожидаемых) значений. Для этого нам нужно рассчитать каждый элемент в новой таблице как:
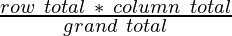
Таблица ожидаемых значений:
| собака | Кот | птица | общее | |
| люди | 223,87343533 | 266.00834492 | 240.11821975 | 730 |
| женщины | 217.12656467 | 257,99165508 | 232,88178025 | 708 |
| общее | 441 | 524 | 473 | 1438 |
Таблица хи-квадрат:
Мы составляем эту таблицу, рассчитывая по каждому пункту следующее:
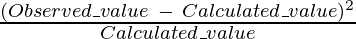
Таблица хи-квадрат:
| наблюдается (о) | рассчитано (c) | (oc) ^ 2 / c | |
| 207 | 223,87343533 | 1,2717579435607573 | |
| 282 | 266.00834492 | 0,9613722161954465 | |
| 241 | 240.11821975 | 0,003238139990850831 | |
| 234 | 217.12656467 | 1,3112758457617977 | |
| 242 | 257,99165508 | 0,991245364156322 | |
| 232 | 232,88178025 | 0,0033387601600580606 | |
| Общее | 4,542228269825232 |
Из этой таблицы мы получаем сумму последнего столбца, которая дает рассчитанное значение хи-квадрат. Следовательно, рассчитанное значение хи-квадрат составляет 4,542228269825232.
Теперь нам нужно найти критическое значение хи-квадрат. Мы можем получить это из таблицы. Чтобы использовать эту таблицу, нам нужно знать степени свободы для набора данных. Степени свободы определяются как: (количество строк - 1) * (количество столбцов - 1).
Следовательно, степени свободы (2-1) * (3-1) = 2
Теперь давайте посмотрим на таблицу и найдем значение, соответствующее 2 степеням свободы и коэффициенту значимости 0,05:
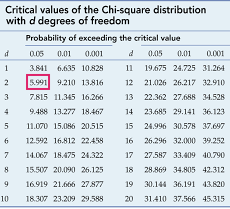
Табличное или критическое значение хи-квадрат здесь составляет 5,991.
Следовательно,
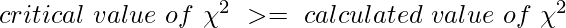
Следовательно, принимается H0 , то есть переменные не имеют существенной связи.
Затем давайте посмотрим, как выполнить тест на Python.
Выполнение теста с использованием Python (scipy.stats):
SciPy - это библиотека Python с открытым исходным кодом, которая используется в математике, инженерии, научных и технических вычислениях.
Монтаж:
pip install scipy
Функция chi2_contingency () модуля scipy.stats принимает в качестве входных данных таблицу непредвиденных обстоятельств в формате 2d-массива. Он возвращает кортеж, содержащий статистику теста , p-значение , степени свободы и ожидаемую таблицу (ту, которую мы создали из вычисленных значений) в указанном порядке.
Следовательно, нам нужно сравнить полученное значение p со значением альфа 0,05.
from scipy.stats import chi2_contingency # defining the tabledata = [[ 207 , 282 , 241 ], [ 234 , 242 , 232 ]]stat, p, dof, expected = chi2_contingency(data) # interpret p-valuealpha = 0.05print ( "p value is " + str (p))if p < = alpha: print ( 'Dependent (reject H0)' )else : print ( 'Independent (H0 holds true)' ) |
Выход :
Значение p равно 0,1031971404730939 Независимый (верно H0)
С,
p-value > alpha
Поэтому мы принимаем H0, то есть переменные не имеют существенной связи.
Внимание компьютерщик! Укрепите свои основы с помощью базового курса программирования Python и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS. А чтобы начать свое путешествие по машинному обучению, присоединяйтесь к курсу Машинное обучение - базовый уровень.