Преимущества и недостатки различных моделей регрессии

Регрессия - это типичная контролируемая обучающая задача. Он используется в тех случаях, когда прогнозируемое значение является непрерывным. Например, мы используем регрессию для прогнозирования целевого числового значения, такого как цена автомобиля, с учетом набора характеристик или предикторов (пробег, марка, возраст). Мы обучаем систему на множестве примеров автомобилей, включая как предикторы, так и соответствующую цену автомобиля (ярлыки).

Типы регрессионных моделей:

• Простая линейная регрессия - это модель линейной регрессии, которая оценивает связь между одной независимой переменной и одной зависимой переменной с помощью прямой линии.
  Пример: Заработная плата = ₀ + ₁ * Опыт ( y = a 0 + a 1 x форма).
• Множественная линейная регрессия - это модель линейной регрессии, которая оценивает взаимосвязь между несколькими независимыми переменными (характеристиками) и одной зависимой переменной.
  Пример: Цена автомобиля = a ₀ + a ₁ * Пробег + a ₂ * Марка + a ₃ * Возраст ( y = a 0 + a 1 x 1 + a 2 x 2 + ... + a n x n форма y = a 0 + a 1 x 1 + a 2 x 2 + ... + a n x n
• Полиномиальная регрессия - это частный случай множественной линейной регрессии. Связь между независимой переменной x и зависимой переменной y моделируется как полином n-й степени от x. Линейная регрессия не может использоваться для подгонки нелинейных данных (недостаточная подгонка). Поэтому мы увеличиваем сложность модели и используем полиномиальную регрессию, которая лучше подходит для таких данных. ( y = a 0 + a 1 x 1 + a 2 x 1 2 + ... + a n x 1 n форма)
• Регрессия опорного вектора - это модель регрессии, в которой мы пытаемся подогнать ошибку к определенному порогу (в отличие от минимизации частоты ошибок, которую мы делали в предыдущих случаях). SVR может работать как с линейными, так и с нелинейными задачами, в зависимости от выбранного ядра. Между переменными существует неявная взаимосвязь, в отличие от предыдущих моделей, где взаимосвязь явно определялась уравнением (коэффициентов достаточно, чтобы сбалансировать шкалу переменных). Следовательно, здесь требуется масштабирование функции.
• Decision Tree Regression строит регрессионную модель в виде древовидной структуры. Поскольку набор данных разбивается на более мелкие подмножества, связанное дерево решений строится постепенно. Для точки в тестовом наборе мы прогнозируем значение, используя построенное дерево решений.
• Регрессия случайного леса - здесь мы берем k точек данных из обучающего набора и строим дерево решений. Мы повторяем это для разных наборов из k точек. Мы должны определить количество деревьев решений, которые будут построены указанным выше способом. Пусть количество построенных деревьев равно n. Мы прогнозируем значение, используя все n деревьев, и берем их среднее значение, чтобы получить окончательное предсказанное значение для точки в тестовом наборе.

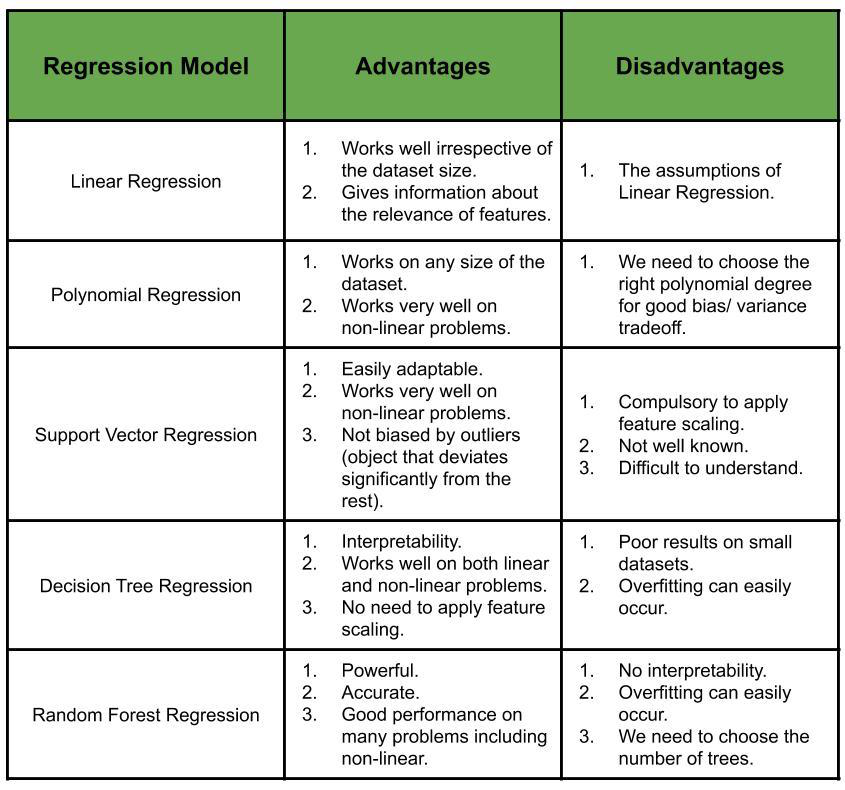
Как выбрать правильную модель регрессии для данной проблемы?
Принимая во внимание такие факторы, как тип связи между зависимой переменной и независимыми переменными (линейная или нелинейная), плюсы и минусы выбора конкретной регрессионной модели для проблемы и ^{интуиция Скорректированного R 2} , мы выбираем регрессию. модель, которая наиболее подходит для решения проблемы.