Построение комбинационных схем

Комбинационная схема состоит из логических элементов, выходы которых в любой момент времени определяются непосредственно из текущей комбинации входов без учета предыдущего входа. Примеры комбинационных схем: сумматор, вычитатель, преобразователь и кодировщик / декодер.

Здесь мы узнаем, как построить и проанализировать любой тип комбинационной схемы, используя четыре основных шага. Я собираюсь объяснить этот трюк с помощью одной комбинационной схемы, и вы можете применить то же самое для реализации других комбинационных схем.

Ниже приведены четыре шага для построения и анализа любой комбинационной схемы.

• Шаг 1: Определите количество входов и выходов схемы.
  Прежде всего, мы должны подумать о входах и выходах схемы, учитывая, какой тип логической операции мы хотим выполнить со схемой.
  Например, нам нужно создать схему, которая может складывать два бита. Для этого нам потребуются два входа (один для первого бита (A), другой для второго бита (B)) и два выхода: один для суммы (S) двух битов, а другой - для переноса (C).

  Всего нам потребуется 2 входа и 2 выхода. Итак, наш первый шаг завершен.

• Шаг 2: Создание таблицы истинности.
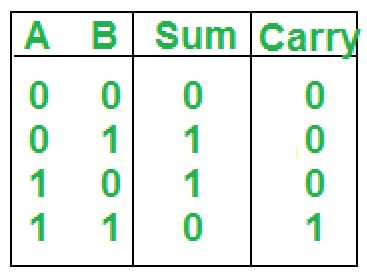
  На этом этапе мы должны создать таблицу истинности для нашей схемы, поэтому для этого сначала мы создадим входные столбцы и перечислим все возможные комбинации входов. В нашем случае 2 бита могут иметь максимум 4 комбинации (00 01 10 11) .
  Теперь на выходе у нас есть два столбца (Sum и Carry), как обсуждалось ранее. Теперь нам нужно заполнить выходные столбцы таким образом, чтобы для какой логической операции мы строим схему.

  В нашей схеме мы хотим сложить, поэтому мы добавим эти входные биты и запишем сумму этих битов в столбец (Sum), и если перенос будет сгенерирован, мы будем писать 1 else write.

  0 в столбце (Перенести).

  

• Шаг 3: Упростите логическую функцию для каждого выхода.
  На этом шаге нам нужно просто создать упрощенную логическую функцию в соответствии с входными и выходными данными таблицы истинности, полученной на предыдущем шаге.
  Для суммы,

   Сумма = A'B + AB '= A XOR B

  Для переноски,

   Перенести = AB = A И B

• Шаг 4: Построение схемы с использованием логической функции, полученной на третьем шаге.
  В сумме мы получили (A XOR B), поэтому мы подключим A и B ко входам логического элемента XOR и возьмем его выход как сумму. Для переноса мы получили (A AND B), поэтому мы подключим A и B ко входам логического элемента AND и возьмем его выход как перенос.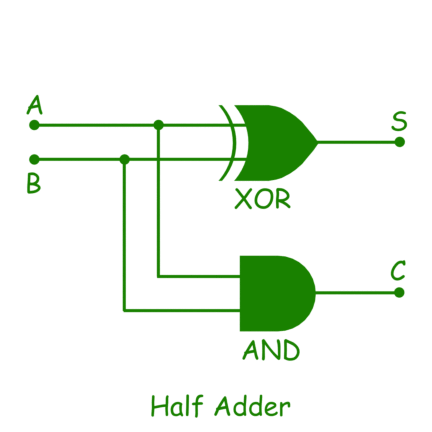

  

  Теперь в этой схеме, если вы обеспечите ввод на концах A и B. Вы получите результат по сумме и переносу в соответствии с таблицей истинности, которую мы создали выше. Итак, мы завершили четыре шага по созданию комбинационной схемы.

Итак, мы создали комбинационную схему под названием Half Adder . Вы можете применить те же шаги для создания любой другой комбинационной схемы.