Поправка Шеппарда для моментов | ML
Предпосылка: сырые и центральные моменты
В сгруппированных данных мы предполагаем, что частоты сосредоточены в средней части классового интервала. Это предположение в общем случае неверно, и возникает ошибка группировки . Такой эффект можно исправить при расчете моментов, используя информацию о ширине интервала классов.
Поправка Шеппарда для ошибки группировки - это не что иное, как корректировка вычисленных моментов выборки для сгруппированных данных или непрерывных данных. Профессор У. Ф. Шеппард доказал, что если частотное распределение является непрерывным и частота сужается до нуля в обоих направлениях, ошибку группирования можно исправить следующим образом:
Пусть 'c' будет шириной интервала между классами. Потом,
Сырые моменты 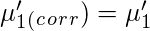
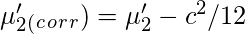
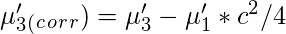
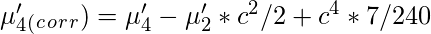
Центральные моменты 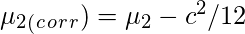
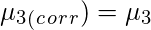
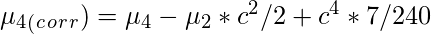
Какие данные можно исправить?
- Этот метод корректировки моментов возможен только для непрерывных переменных, то есть непрерывных данных.
- Ширина классного интервала должна быть одинаковой.
- Частоты должны быть симметричными. Частота должна снижаться до нуля в обоих направлениях.
Учитывайте данное распределение оценок.
| Метки | Количество студентов |
|---|---|
| 0–10 | 1 |
| 10–20 | 6 |
| 20–30 | 11 |
| 30–40 | 17 |
| 40–50 | 21 год |
| 50–60 | 16 |
| 60 - 70 | 13 |
| 70 - 80 | 7 |
| 80 - 90 | 5 |
| 90–100 | 2 |
Для распределения оценок выше значения моментов указаны ниже:
Сырые моменты - 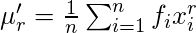 , - r-й необработанный момент, где
, - r-й необработанный момент, где 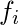 это частота и
это частота и 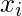 это среднее значение класса.
это среднее значение класса.
Итак, используя приведенную выше формулу для исходного момента, мы получаем следующие значения для моментов. 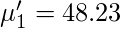
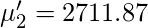
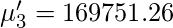
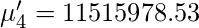
Поправка Шеппарда для сырых моментов -
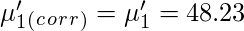
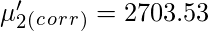
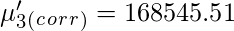
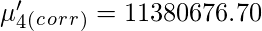
Аналогичным образом центральные моменты можно исправить с помощью поправки Шеппарда .