Понимание логистической регрессии

Опубликовано: 14 Июля, 2021

Предпосылка: линейная регрессия
В этой статье обсуждаются основы логистической регрессии и ее реализация на Python. Логистическая регрессия - это, по сути, алгоритм классификации с учителем. В задаче классификации целевая переменная (или выходные данные) y может принимать только дискретные значения для данного набора функций (или входных данных) X.

Вопреки распространенному мнению, логистическая регрессия ЯВЛЯЕТСЯ регрессионной моделью. Модель строит регрессионную модель для прогнозирования вероятности того, что данная запись данных относится к категории с номером «1». Так же, как линейная регрессия предполагает, что данные подчиняются линейной функции, логистическая регрессия моделирует данные с помощью сигмоидной функции.

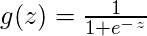
Логистическая регрессия становится методом классификации только тогда, когда появляется порог принятия решения. Установка порогового значения является очень важным аспектом логистической регрессии и зависит от самой проблемы классификации.

Решение о значении порогового значения в значительной степени зависит от значений точности и полноты. В идеале мы хотим, чтобы и точность, и отзыв были равны 1, но это бывает редко. В случае компромисса с точностью до отзыва мы используем следующие аргументы для определения порогового значения:

1. Низкая точность / высокий уровень отзыва. В приложениях, где мы хотим уменьшить количество ложных срабатываний без обязательного уменьшения количества ложных срабатываний, мы выбираем значение решения, которое имеет низкое значение точности или высокое значение отзыва. Например, в приложении для диагностики рака мы не хотим, чтобы какой-либо больной пациент был классифицирован как здоровый, не обращая особого внимания на то, ошибочно ли у пациента диагностирован рак. Это связано с тем, что отсутствие рака может быть обнаружено по другим медицинским заболеваниям, но наличие болезни не может быть обнаружено у уже отвергнутого кандидата.

2. Высокая точность / низкий уровень отзыва. В приложениях, где мы хотим уменьшить количество ложных срабатываний без обязательного уменьшения количества ложноотрицательных результатов, мы выбираем значение решения, которое имеет высокое значение точности или низкое значение отзыва. Например, если мы классифицируем клиентов, будут ли они реагировать положительно или отрицательно на персонализированную рекламу, мы хотим быть абсолютно уверены, что покупатель положительно отреагирует на рекламу, потому что в противном случае отрицательная реакция может привести к потере потенциальных продаж от покупателя. .

По количеству категорий логистическую регрессию можно классифицировать как:

биномиальная: целевая переменная может иметь только 2 возможных типа: «0» или «1», которые могут представлять «выигрыш» против «проигрыша», «пройти» против «неудачи», «мертвый» против «живого» и т. д.
полиномиальная: целевая переменная может иметь 3 или более возможных типов, которые не упорядочены (т. е. типы не имеют количественной значимости), например «болезнь A» против «болезни B» против «болезни C».
порядковый: он имеет дело с целевыми переменными с упорядоченными категориями. Например, результат теста можно разделить на следующие категории: «очень плохо», «плохо», «хорошо», «очень хорошо». Здесь каждой категории можно присвоить оценку 0, 1, 2, 3.

Прежде всего, мы исследуем простейшую форму логистической регрессии, то есть биномиальную логистическую регрессию .

Биномиальная логистическая регрессия

Рассмотрим пример набора данных, который отображает количество часов обучения и результат экзамена. Результат может принимать только два значения, а именно пройдено (1) или не выполнено (0):



Часы (x)
0,50
0,75
1,00
1,25
1,50
1,75
2,00
2,25
2,50
2,75
3,00
3,25
3,50
3,75
4.00
4,25
4,50
4,75
5.00
5,50


Пройдено (у)
0
0
0
0
0
0
1
0
1
0
1
0
1
0
1
1
1
1
1
1

Итак, у нас есть
$y = \left\{\begin{matrix} 0,if fail\\ 1,if pass\\ \end{matrix}\right.$
т.е. y - категориальная целевая переменная, которая может принимать только два возможных типа: «0» или «1».
Чтобы обобщить нашу модель, мы предполагаем, что:

В наборе данных есть переменные признаков «p» и «n» наблюдений.
Матрица признаков представлена как:
$\mathbf{X} =\begin{pmatrix} 1 & x_{11} & \cdots & x_{1p} \\ 1 & x_{21} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & \cdots & x_{np} \end{pmatrix}$
Здесь,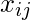 обозначает значения 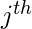особенность для 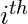наблюдение.
Здесь мы придерживаемся соглашения о разрешении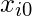 = 1. (Продолжайте читать, через несколько секунд вы поймете логику).
В 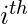наблюдение 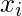, можно представить как:
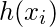$x_i = \begin{bmatrix} 1\\ x_{i1}\\ x_{i2}\\ .\\ .\\ x_{ip}\\ \end{bmatrix}$
представляет собой прогнозируемый ответ для 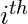наблюдение, т.е. 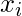. Формула, которую мы используем для расчета 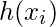называется гипотезой .

Если вы прошли через линейную регрессию, вы должны помнить, что в линейной регрессии гипотеза, которую мы использовали для прогнозирования, была следующей:
$h(x_i) = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} + ..... + \beta_px_{ip}$
где, 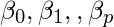- коэффициенты регрессии.
Пусть матрица / вектор коэффициентов регрессии, 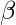быть:
$\beta = \begin{bmatrix} \beta_0\\ \beta_1\\ \beta_2\\ .\\ .\\ \beta_p\\ \end{bmatrix}$
Тогда в более компактном виде
$h(x_i) = \beta^Tx_i$

The reason for taking = 1 is pretty clear now.
We needed to do a matrix product, but there was no
actual multiplied to in original hypothesis formula. So, we defined = 1.

Теперь, если мы попытаемся применить линейную регрессию к указанной выше проблеме, мы, вероятно, получим непрерывные значения, используя гипотезу, которую мы обсуждали выше. Кроме того, это не имеет смысла для 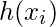принимать значения больше 1 или меньше 0.
Итак, в гипотезу классификации внесены некоторые изменения:
$h(x_i) = g(\beta^T x_i) = \frac{1}{1 + e^{-\beta^T x_i}}$
где,
$g(z) = \frac{1}{1 + e^{-z}}$
называется логистической функцией или сигмовидной функцией .
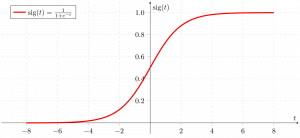
Вот график, показывающий g (z):

Из приведенного выше графика мы можем вывести, что:

g (z) стремится к 1 при
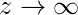
g (z) стремится к 0 при
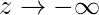
g (z) всегда ограничен между 0 и 1

Итак, теперь мы можем определить условные вероятности для 2 меток (0 и 1) для 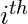наблюдение как:
$\newline P(y_i = 1|x_i; \beta) = h(x_i) \newline P(y_i=0|x_i; \beta) = 1 - h(x_i)$
Мы можем записать это более компактно:
$P(y_i|x_i;\beta) = (h(x_i))^{y_i}(1-h(x_i))^{1-y_i}$
Теперь мы определяем еще один термин, вероятность параметров, как:
$\newline L(\beta) = \prod_{i=1}^{n}P(y_i|x_i;\beta) \newline or \newline L(\beta) = \prod_{i=1}^{n}(h(x_i))^{y_i}(1-h(x_i))^{1-y_i}$

Likelihood is nothing but the probability of data(training examples), given a model and specific parameter values(here, ). It measures the support provided by the data for each possible value of the . We obtain it by multiplying all for given .

А для упрощения расчетов берем логарифмическую вероятность :
$\newline l(\beta) = log(L(\beta)) \newline or \newline l(\beta) = \sum_{i=1}^{n}y_ilog(h(x_i)) + (1-y_i)log(1-h(x_i))$
Функция стоимости для логистической регрессии пропорциональна обратной величине вероятности параметров. Следовательно, мы можем получить выражение для функции стоимости J, используя уравнение логарифмического правдоподобия:
$J(\beta) =\sum_{i=1}^{n} - y_ilog(h(x_i)) - (1-y_i)log(1-h(x_i))$
и наша цель - оценить 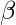так что функция стоимости минимизирована !!

Использование алгоритма градиентного спуска

Сначала возьмем частные производные от 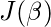по каждому 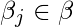для вывода правила стохастического градиентного спуска (здесь мы представляем только окончательное производное значение):
$\frac{\partial J(\beta)}{\partial \beta_j} = (h(x) - y)x_j$
Здесь y и h (x) представляют вектор отклика и прогнозируемый вектор отклика (соответственно). Также, 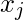- вектор, представляющий значения наблюдений для 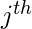характерная черта.
Теперь, чтобы получить мин. ,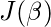
$\newline Repeat\{ \newline \beta_j := \beta_j - \alpha\sum_{i=1}^{n}(h(x_i)-y_i)x_{ij} \newline (Simultaneously\hspace{5}update\hspace{5}all\hspace{5}\beta_j) \newline \}$
где 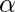называется скоростью обучения и требует явной настройки.
Давайте посмотрим на реализацию вышеуказанного метода на Python на примере набора данных (загрузите его отсюда):

2,252,502,753,003,253,503,754.004,254,504,755.005,50

 import csv
 import numpy as np
 import matplotlib.pyplot as plt
 
 
def loadCSV(filename):
    '''
    function to load dataset
    '''
    with open (filename, "r" ) as csvfile:
        lines = csv.reader(csvfile)
        dataset = list (lines)
        for i in range ( len (dataset)):
            dataset[i] = [ float (x) for x in dataset[i]]
    return np.array(dataset)
 
 
def normalize(X):
    '''
    function to normalize feature matrix, X
    '''
    mins = np. min (X, axis = 0 )
    maxs = np. max (X, axis = 0 )
    rng = maxs - mins
    norm_X = 1 - ((maxs - X) / rng)
    return norm_X
 
 
def logistic_func(beta, X):
    '''
    logistic(sigmoid) function
    '''
    return 1.0 / ( 1 + np.exp( - np.dot(X, beta.T)))
 
 
def log_gradient(beta, X, y):
    '''
    logistic gradient function
    '''
    first_calc = logistic_func(beta, X) - y.reshape(X.shape[ 0 ], - 1 )
    final_calc = np.dot(first_calc.T, X)
    return final_calc
 
 
def cost_func(beta, X, y):
    '''
    cost function, J
    '''
    log_func_v = logistic_func(beta, X)
    y = np.squeeze(y)
    step1 = y * np.log(log_func_v)
    step2 = ( 1 - y) * np.log( 1 - log_func_v)
    final = - step1 - step2
    return np.mean(final)
 
 
def grad_desc(X, y, beta, lr = . 01 , converge_change = . 001 ):
    '''
    gradient descent function
    '''
    cost = cost_func(beta, X, y)
    change_cost = 1
    num_iter = 1
     
    while (change_cost > converge_change):
        old_cost = cost
        beta = beta - (lr * log_gradient(beta, X, y))
        cost = cost_func(beta, X, y)
        change_cost = old_cost - cost
        num_iter + = 1
     
    return beta, num_iter
 
 
def pred_values(beta, X):
    '''
    function to predict labels
    '''
    pred_prob = logistic_func(beta, X)
    pred_value = np.where(pred_prob > = . 5 , 1 , 0 )
    return np.squeeze(pred_value)
 
 
def plot_reg(X, y, beta):
    '''
    function to plot decision boundary
    '''
    # labelled observations
    x_0 = X[np.where(y = = 0.0 )]
    x_1 = X[np.where(y = = 1.0 )]
     
    # plotting points with diff color for diff label
    plt.scatter([x_0[:, 1 ]], [x_0[:, 2 ]], c = 'b' , label = 'y = 0' )
    plt.scatter([x_1[:, 1 ]], [x_1[:, 2 ]], c = 'r' , label = 'y = 1' )
     
    # plotting decision boundary
    x1 = np.arange( 0 , 1 , 0.1 )
    x2 = - (beta[ 0 , 0 ] + beta[ 0 , 1 ] * x1) / beta[ 0 , 2 ]
    plt.plot(x1, x2, c = 'k' , label = 'reg line' )
 
    plt.xlabel( 'x1' )
    plt.ylabel( 'x2' )
    plt.legend()
    plt.show()
     
 
     
if __name__ = = "__main__" :
    # load the dataset
    dataset = loadCSV( 'dataset1.csv' )
     
    # normalizing feature matrix
    X = normalize(dataset[:, : - 1 ])
     
    # stacking columns wth all ones in feature matrix
    X = np.hstack((np.matrix(np.ones(X.shape[ 0 ])).T, X))
 
    # response vector
    y = dataset[:, - 1 ]
 
    # initial beta values
    beta = np.matrix(np.zeros(X.shape[ 1 ]))
 
    # beta values after running gradient descent
    beta, num_iter = grad_desc(X, y, beta)
 
    # estimated beta values and number of iterations
    print ( "Estimated regression coefficients:" , beta)
    print ( "No. of iterations:" , num_iter)
 
    # predicted labels
    y_pred = pred_values(beta, X)
     
    # number of correctly predicted labels
    print ( "Correctly predicted labels:" , np. sum (y = = y_pred))
     
    # plotting regression line
    plot_reg(X, y, beta)

 Estimated regression coefficients: [[ 1.70474504 15.04062212 -20.47216021]] No. of iterations: 2612 Correctly predicted labels: 100

Примечание. Градиентный спуск - один из многих способов оценки .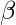
По сути, это более сложные алгоритмы, которые можно легко запустить на Python после того, как вы определили свою функцию стоимости и свои градиенты. Эти алгоритмы:

BFGS (алгоритм Бройдена – Флетчера – Гольдфарба – Шанно)
L-BFGS (как BFGS, но использует ограниченную память)
Сопряженный градиент

Преимущества / недостатки использования любого из этих алгоритмов перед градиентным спуском:

Преимущества
- Не нужно выбирать скорость обучения
- Часто бегают быстрее (не всегда)
- Может численно приблизить градиент для вас (не всегда получается)
Недостатки
- Более сложный
- Скорее черный ящик, если вы не узнаете подробностей

Полиномиальная логистическая регрессия

В полиномиальной логистической регрессии выходная переменная может иметь более двух возможных дискретных выходов . Рассмотрим набор цифр. Здесь выходной переменной является цифровое значение, которое может принимать значения из (0, 12, 3, 4, 5, 6, 7, 8, 9).
Ниже приведена реализация полиномиальной логической регрессии с использованием scikit-learn для прогнозирования набора цифровых данных.

 from sklearn import datasets, linear_model, metrics
  
# load the digit dataset
 digits = datasets.load_digits()
  
# defining feature matrix(X) and response vector(y)
 X = digits.data
 y = digits.target
 
# splitting X and y into training and testing sets
 from sklearn.model_selection import train_test_split
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.4 ,
                                                    random_state = 1 )
  
# create logistic regression object
 reg = linear_model.LogisticRegression()
  
# train the model using the training sets
 reg.fit(X_train, y_train)
 
# making predictions on the testing set
 y_pred = reg.predict(X_test)
  
# comparing actual response values (y_test) with predicted response values (y_pred)
 print ( "Logistic Regression model accuracy(in %):" ,
 metrics.accuracy_score(y_test, y_pred) * 100 ) 

 Logistic Regression model accuracy(in %): 95.6884561892

Наконец, вот некоторые моменты логистической регрессии, над которыми стоит задуматься:

НЕ предполагает линейной связи между зависимой переменной и независимыми переменными, но предполагает линейную связь между логитом независимых переменных и ответом .
Независимые переменные могут быть даже степенными членами или некоторыми другими нелинейными преобразованиями исходных независимых переменных.
Зависимая переменная НЕ обязательно должна иметь нормальное распределение, но обычно предполагает распределение из экспоненциального семейства (например, биномиальное, пуассоновское, полиномиальное, нормальное,…); бинарная логистическая регрессия предполагает биномиальное распределение ответа.
Необязательно удовлетворять однородность дисперсии.
Ошибки должны быть независимыми, но НЕ нормально распределенными.
Он использует оценку максимального правдоподобия (MLE) вместо обычного метода наименьших квадратов (OLS) для оценки параметров и, таким образом, полагается на приближения с большой выборкой .

Рекомендации:

http://cs229.stanford.edu/notes/cs229-notes1.pdf
http://machinelearningmaster.com/logistic-regression-for-machine-learning/
https://onlinecourses.science.psu.edu/stat504/node/164

Эта статья предоставлена Нихилом Кумаром . Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью с помощью provide.geeksforgeeks.org или отправить ее по электронной почте на deposit@geeksforgeeks.org. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам.

Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше.

Внимание компьютерщик! Укрепите свои основы с помощью базового курса программирования Python и изучите основы.

Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS. А чтобы начать свое путешествие по машинному обучению, присоединяйтесь к курсу Машинное обучение - базовый уровень.

Python Машинное обучение Продвинутая компьютерная тематика

Часы (x)	0,50	0,75	1,00	1,25	1,50	1,75	2,00	2,25	2,50	2,75	3,00	3,25	3,50	3,75	4.00	4,25	4,50	4,75	5.00	5,50
Пройдено (у)	0	0	0	0	0	0	1	0	1	0	1	0	1	0	1	1	1	1	1	1

Понимание логистической регрессии

РЕКОМЕНДУЕМЫЕ СТАТЬИ