Наивные байесовские классификаторы
В этой статье обсуждается теория, лежащая в основе наивных байесовских классификаторов, и их реализация.
Наивные байесовские классификаторы - это набор алгоритмов классификации, основанных на теореме Байеса . Это не единый алгоритм, а семейство алгоритмов, в которых все они разделяют общий принцип, т.е. каждая пара классифицируемых признаков не зависит друг от друга.
Для начала рассмотрим набор данных.
Рассмотрим вымышленный набор данных, описывающий погодные условия для игры в гольф. Учитывая погодные условия, каждый набор классифицирует условия как пригодные («Да») или непригодные («Нет») для игры в гольф.
Вот табличное представление нашего набора данных.
| Перспективы | Температура | Влажность | Ветреный | Играть в гольф | |
|---|---|---|---|---|---|
| 0 | Дождливый | Горячий | Высокая | Ложь | Нет |
| 1 | Дождливый | Горячий | Высокая | Правда | Нет |
| 2 | Пасмурная погода | Горячий | Высокая | Ложь | да |
| 3 | Солнечно | Мягкий | Высокая | Ложь | да |
| 4 | Солнечно | Прохладный | Обычный | Ложь | да |
| 5 | Солнечно | Прохладный | Обычный | Правда | Нет |
| 6 | Пасмурная погода | Прохладный | Обычный | Правда | да |
| 7 | Дождливый | Мягкий | Высокая | Ложь | Нет |
| 8 | Дождливый | Прохладный | Обычный | Ложь | да |
| 9 | Солнечно | Мягкий | Обычный | Ложь | да |
| 10 | Дождливый | Мягкий | Обычный | Правда | да |
| 11 | Пасмурная погода | Мягкий | Высокая | Правда | да |
| 12 | Пасмурная погода | Горячий | Обычный | Ложь | да |
| 13 | Солнечно | Мягкий | Высокая | Правда | Нет |
Набор данных разделен на две части: матрицу признаков и вектор ответа .
- Матрица признаков содержит все векторы (строки) набора данных, в которых каждый вектор состоит из значений зависимых признаков . В приведенном выше наборе данных это «Outlook», «Температура», «Влажность» и «Ветреный ветер».
- Вектор ответа содержит значение переменной класса (прогноз или результат) для каждой строки матрицы признаков. В приведенном выше наборе данных имя переменной класса - «Играть в гольф».
Предположение:
Фундаментальное предположение Наивного Байеса состоит в том, что каждая функция создает:
- независимый
- равный
вклад в результат.
Применительно к нашему набору данных эту концепцию можно понять как:
- Мы предполагаем, что никакая пара функций не является зависимой. Например, «высокая» температура не имеет ничего общего с влажностью, или «дождливый» прогноз не влияет на ветер. Следовательно, предполагается, что функции независимы .
- Во-вторых, каждой функции присваивается одинаковый вес (или важность). Например, зная только температуру и влажность, нельзя точно предсказать результат. Ни один из атрибутов не имеет значения и предполагается, что они в равной степени влияют на результат.
Примечание: предположения, сделанные Наивным Байесом, обычно неверны в реальных ситуациях. Фактически, предположение о независимости никогда не бывает правильным, но часто хорошо работает на практике.
Теперь, прежде чем перейти к формуле наивного Байеса, важно знать о теореме Байеса.
Теорема Байеса
Теорема Байеса определяет вероятность наступления события с учетом вероятности другого события, которое уже произошло. Теорема Байеса математически формулируется в виде следующего уравнения:
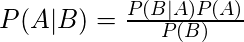
где A и B - события и P (B)? 0.
- По сути, мы пытаемся найти вероятность события A, если событие B истинно. Событие B также называется свидетельством .
- P (A) - это априорная вероятность A (априорная вероятность, т. Е. Вероятность события до того, как будет видно свидетельство). Свидетельство - это значение атрибута неизвестного экземпляра (здесь это событие B).
- P (A | B) - это апостериорная вероятность B, то есть вероятность события после того, как будет обнаружено свидетельство.
Теперь, что касается нашего набора данных, мы можем применить теорему Байеса следующим образом:
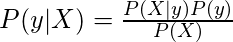
где y - переменная класса, а X - зависимый вектор признаков (размера n ), где:
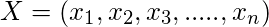
Чтобы прояснить, примером вектора признаков и соответствующей переменной класса может быть: (см. 1-ю строку набора данных)
X = (Rainy, Hot, High, False) y = NoТаким образом, P (y | X) здесь означает вероятность «Не играть в гольф», учитывая, что погодные условия следующие: «Дождь», «Высокая температура», «Высокая влажность» и «Без ветра».
Наивное предположение
Теперь пришло время сделать наивное предположение теоремы Байеса о независимости между функциями. Итак, теперь мы разделяем доказательства на независимые части.
Теперь, если любые два события A и B независимы, то
P(A,B) = P(A)P(B)Отсюда и приходим к результату:
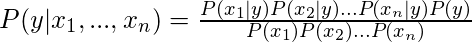
что может быть выражено как:
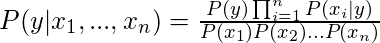
Теперь, когда знаменатель остается постоянным для данного ввода, мы можем удалить этот член:
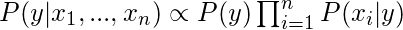
Теперь нам нужно создать модель классификатора. Для этого мы находим вероятность данного набора входов для всех возможных значений переменной класса y и выбираем выход с максимальной вероятностью. Математически это можно выразить как:
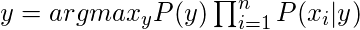
Итак, наконец, нам остается вычислить P (y) и P (x i | y).
Обратите внимание, что P (y) также называется вероятностью класса, а P (x i | y) называется условной вероятностью .
Различные наивные байесовские классификаторы различаются в основном предположениями, которые они делают относительно распределения P (x i | y).
Давайте попробуем применить приведенную выше формулу вручную к нашему набору данных о погоде. Для этого нам нужно выполнить некоторые предварительные вычисления для нашего набора данных.
Нам нужно найти P (x i | y j ) для каждого x i в X и y j в y. Все эти расчеты продемонстрированы в таблицах ниже:
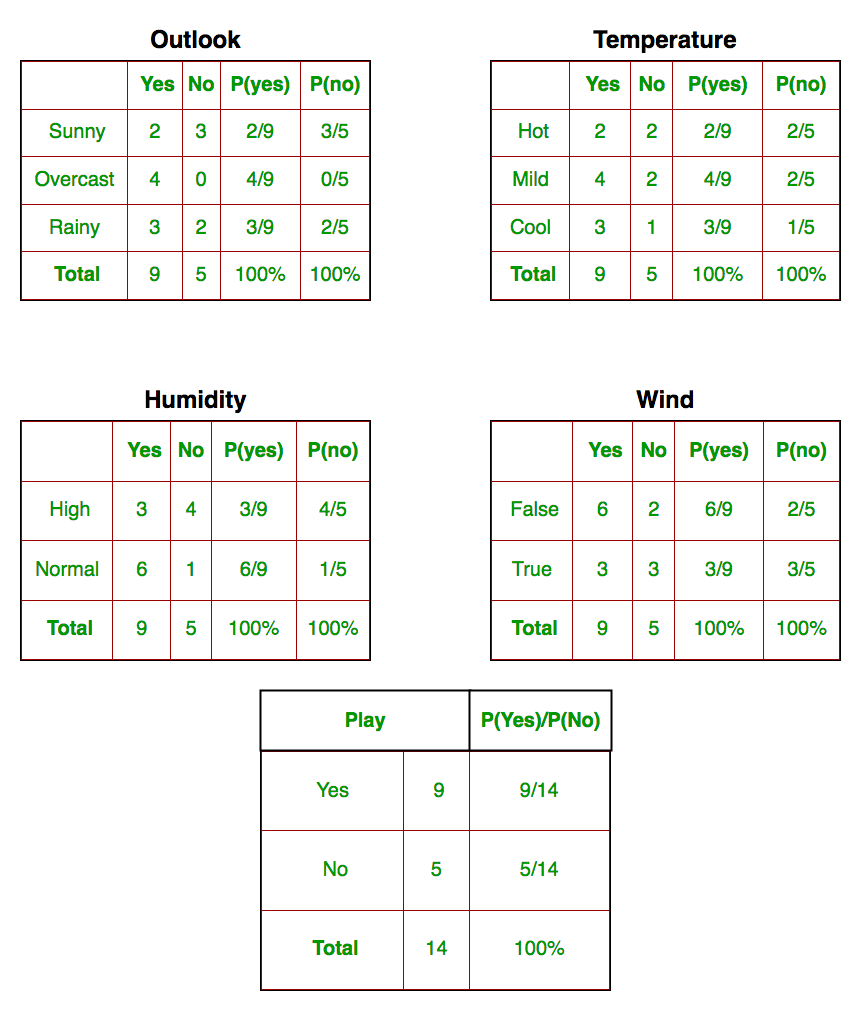
Итак, на рисунке выше мы вычислили P (x i | y j ) для каждого x i в X и y j в y вручную в таблицах 1-4. Например, вероятность игры в гольф при низкой температуре, то есть P (темп. = Прохладно | играть в гольф = Да) = 3/9.
Кроме того, нам нужно найти вероятности классов (P (y)), которые были вычислены в таблице 5. Например, P (играть в гольф = Да) = 9/14.
Итак, мы закончили наши предварительные вычисления, и классификатор готов!
Давайте протестируем его на новом наборе функций (назовем его сегодня):
today = (Sunny, Hot, Normal, False)Итак, вероятность игры в гольф определяется по формуле:
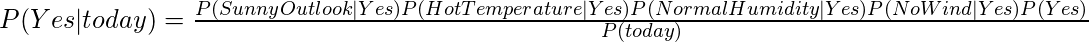
а вероятность не играть в гольф определяется по формуле:

Поскольку P (сегодня) является общим для обеих вероятностей, мы можем игнорировать P (сегодня) и найти пропорциональные вероятности как:
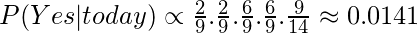
а также
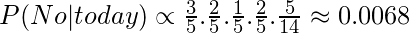
Теперь, поскольку
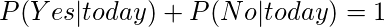
Эти числа можно преобразовать в вероятность, сделав сумму равной 1 (нормализация):
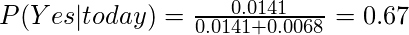
а также
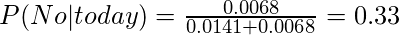
С

Итак, предсказание, что в гольф будут играть - «Да».
Метод, который мы обсуждали выше, применим для дискретных данных. В случае непрерывных данных нам необходимо сделать некоторые предположения относительно распределения значений каждой функции. Различные наивные байесовские классификаторы различаются в основном предположениями, которые они делают относительно распределения P (x i | y).
Теперь мы обсудим здесь один из таких классификаторов.
Гауссовский наивный байесовский классификатор
В гауссовском наивном байесовском методе предполагается, что непрерывные значения, связанные с каждой функцией, распределены согласно гауссовскому распределению . Распределение Гаусса также называется нормальным распределением. При построении он дает колоколообразную кривую, которая симметрична среднему значению характеристик, как показано ниже:
Предполагается, что вероятность появления признаков является гауссовой, следовательно, условная вероятность определяется как:
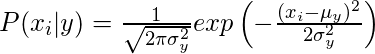
Теперь мы рассмотрим реализацию гауссовского наивного байесовского классификатора с помощью scikit-learn.
# load the iris datasetfrom sklearn.datasets import load_irisiris = load_iris() # store the feature matrix (X) and response vector (y)X = iris.datay = iris.target # splitting X and y into training and testing setsfrom sklearn.model_selection import train_test_splitX_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.4 , random_state = 1 ) # training the model on training setfrom sklearn.naive_bayes import GaussianNBgnb = GaussianNB()gnb.fit(X_train, y_train) # making predictions on the testing sety_pred = gnb.predict(X_test) # comparing actual response values (y_test) with predicted response values (y_pred)from sklearn import metricsprint ( "Gaussian Naive Bayes model accuracy(in %):" , metrics.accuracy_score(y_test, y_pred) * 100 ) |
Выход:
Точность гауссовской наивной байесовской модели (в%): 95,0
Другие популярные наивные байесовские классификаторы:
- Полиномиальный наивный байесовский анализ : векторы признаков представляют частоты, с которыми определенные события были сгенерированы полиномиальным распределением . Это модель событий, обычно используемая для классификации документов.
- Бернулли Наивный Байес : в многомерной модели событий Бернулли функции являются независимыми логическими значениями (двоичными переменными), описывающими входные данные. Как и полиномиальная модель, эта модель популярна для задач классификации документов, где используются особенности вхождения бинарного термина (то есть слово встречается в документе или нет), а не частота терминов (то есть частота слова в документе).
Когда мы дойдем до конца этой статьи, вот несколько важных моментов, над которыми стоит задуматься:
- Несмотря на свои явно чрезмерно упрощенные предположения, наивные байесовские классификаторы довольно хорошо работают во многих реальных ситуациях, хорошо документируя классификацию и фильтрацию спама. Им требуется небольшой объем обучающих данных для оценки необходимых параметров.
- Наивные Байесовские ученики и классификаторы могут быть чрезвычайно быстрыми по сравнению с более сложными методами. Разделение условных распределений признаков классов означает, что каждое распределение может быть независимо оценено как одномерное распределение. Это, в свою очередь, помогает облегчить проблемы, возникающие из-за проклятия размерности.
Рекомендации:
- https://en.wikipedia.org/wiki/Naive_Bayes_classifier
- http://gerardnico.com/wiki/data_mining/naive_bayes
- http://scikit-learn.org/stable/modules/naive_bayes.html
Этот блог предоставлен Нихилом Кумаром. Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью с помощью provide.geeksforgeeks.org или отправить ее по электронной почте на deposit@geeksforgeeks.org. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам.
Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше.
Внимание компьютерщик! Укрепите свои основы с помощью базового курса программирования Python и изучите основы.
Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS. А чтобы начать свое путешествие по машинному обучению, присоединяйтесь к курсу Машинное обучение - базовый уровень.