Множественная линейная регрессия с использованием R
Предпосылка: простая линейная регрессия с использованием R
Линейная регрессия:
Это основной и часто используемый тип для прогнозного анализа. Это статистический подход для моделирования взаимосвязи между зависимой переменной и заданным набором независимых переменных.
Они бывают двух типов:
- Простая линейная регрессия
- Множественная линейная регрессия
Давайте обсудим множественную линейную регрессию с использованием R.
Множественная линейная регрессия:
Это наиболее распространенная форма линейной регрессии. Множественная линейная регрессия в основном описывает, как переменная одного отклика Y линейно зависит от ряда переменных-предикторов.
Основные примеры использования множественной регрессии:
- Цена продажи дома может зависеть от желаемого местоположения, количества спален, количества ванных комнат, года постройки дома, площади участка и ряда других факторов.
- Рост ребенка может зависеть от роста матери, роста отца, питания и факторов окружающей среды.
Оценка параметров модели.
Рассмотрим модель множественной линейной регрессии с k независимыми предикторами x1, x2 ……, xk и одной переменной отклика y.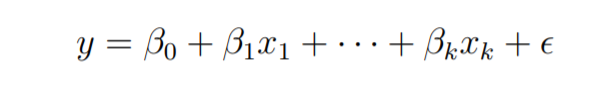
Предположим, у нас есть n наблюдений для k + 1 переменных, и переменная n должна быть больше k.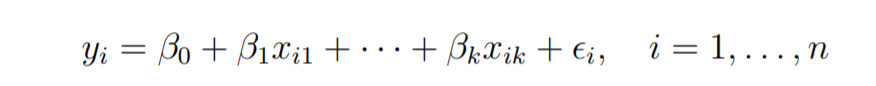
Основная цель регрессии методом наименьших квадратов - подогнать гиперплоскость в (k + 1) -мерное пространство, которое минимизирует сумму квадратов остатков.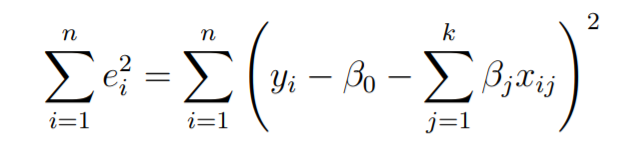
Прежде чем брать производную по параметрам модели, установите их равными нулю и выведите нормальные уравнения наименьших квадратов, которым параметры должны будут удовлетворять.
Эти уравнения формулируются с помощью векторов и матриц.
Позволять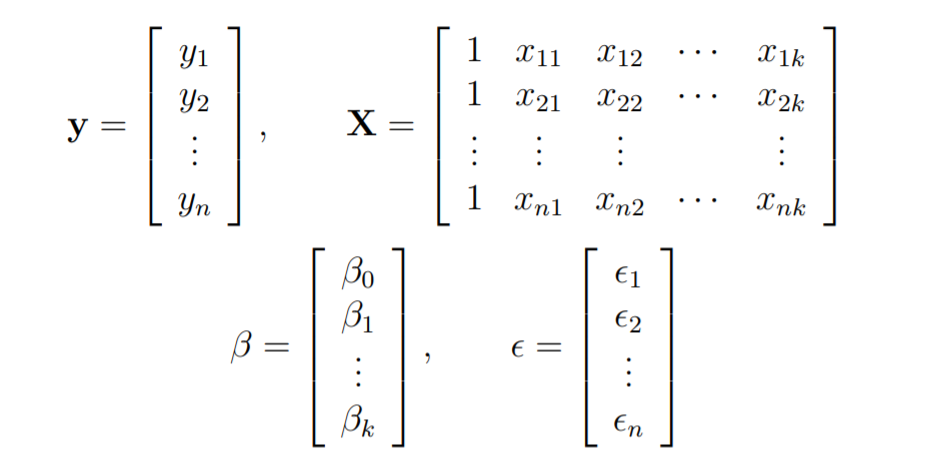
Модель линейной регрессии записывается в следующем виде: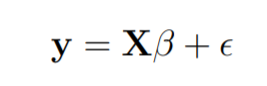
В линейной регрессии оценки параметров методом наименьших квадратов b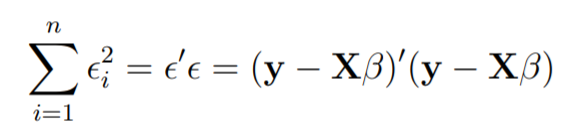
Представьте, что столбцы X фиксированы, они представляют собой данные для конкретной проблемы, а, скажем, b - переменная. Мы хотим найти «лучший» b в том смысле, что сумма квадратов остатков минимизирована.
Наименьшее возможное значение суммы квадратов равно нулю.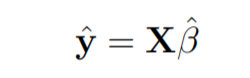
Здесь y - предполагаемый вектор отклика.
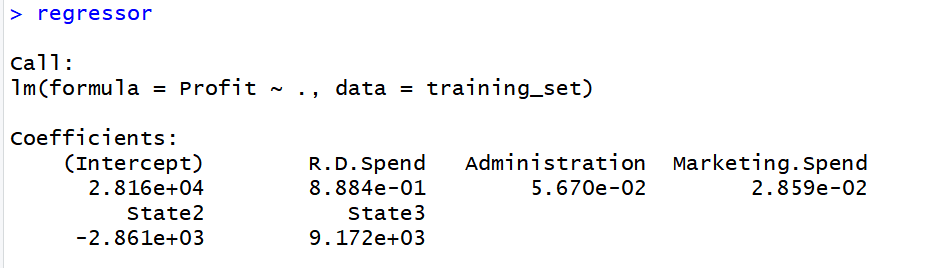
Следующий код R используется для реализации множественной линейной регрессии для следующего набора данных2.
набор данных выглядит так: 
# Multiple Linear Regression # Importing the datasetdataset = read.csv ( 'data2.csv' ) # Encoding categorical datadataset$State = factor (dataset$State, levels = c ( 'New York' , 'California' , 'Florida' ), labels = c (1, 2, 3))dataset$State |

# Splitting the dataset into the Training set and Test set# install.packages('caTools')library (caTools)set.seed (123)split = sample.split (dataset$Profit, SplitRatio = 0.8)training_set = subset (dataset, split == TRUE )test_set = subset (dataset, split == FALSE ) # Feature Scaling# training_set = scale(training_set)# test_set = scale(test_set) # Fitting Multiple Linear Regression to the Training setregressor = lm (formula = Profit ~ ., data = training_set) # Predicting the Test set resultsy_pred = predict (regressor, newdata = test_set) |
Выход: