ML | Стохастический градиентный спуск (SGD)

Опубликовано: 25 Июля, 2021

Что такое градиентный спуск?
Прежде чем объяснять стохастический градиентный спуск (SGD), давайте сначала опишем, что такое градиентный спуск. Градиентный спуск - это популярный метод оптимизации в машинном обучении и глубоком обучении, который можно использовать с большинством, если не всеми, алгоритмами обучения. Градиент - это наклон функции. Он измеряет степень изменения переменной в ответ на изменения другой переменной. Математически градиентный спуск - это выпуклая функция, выход которой является частной производной набора параметров входных данных. Чем больше уклон, тем круче уклон.

Начиная с начального значения, Gradient Descent запускается итеративно, чтобы найти оптимальные значения параметров, чтобы найти минимально возможное значение заданной функции стоимости.

Типы градиентного спуска:
Обычно существует три типа градиентного спуска:

Пакетный градиентный спуск
Стохастический градиентный спуск
Мини-пакетный градиентный спуск

В этой статье мы обсудим стохастический градиентный спуск или SGD.

Стохастический градиентный спуск (SGD):

Слово « стохастический » означает систему или процесс, связанный со случайной вероятностью. Следовательно, в стохастическом градиентном спуске несколько выборок выбираются случайным образом вместо всего набора данных для каждой итерации. В «Градиентном спуске» есть термин «пакет», который обозначает общее количество выборок из набора данных, который используется для вычисления градиента для каждой итерации. При типичной оптимизации градиентного спуска, такой как пакетный градиентный спуск, пакетом считается весь набор данных. Хотя использование всего набора данных действительно полезно для достижения минимумов менее шумным и менее случайным образом, но проблема возникает, когда наши наборы данных становятся большими.
Предположим, у вас есть миллион выборок в вашем наборе данных, поэтому, если вы используете типичную технику оптимизации градиентного спуска, вам придется использовать весь миллион выборок для выполнения одной итерации при выполнении градиентного спуска, и это должно быть сделано для каждую итерацию до достижения минимумов. Следовательно, выполнение этого становится очень дорогостоящим в вычислительном отношении.

Эта проблема решается методом стохастического градиентного спуска. В SGD для выполнения каждой итерации используется только одна выборка, т. Е. Пакет размером один. Выборка случайным образом перемешивается и выбирается для выполнения итерации.

Алгоритм SGD:

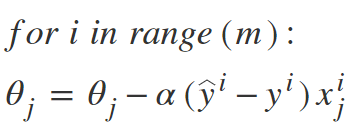
Итак, в SGD мы находим градиент функции стоимости одного примера на каждой итерации вместо суммы градиента функции стоимости всех примеров.

В SGD, поскольку для каждой итерации случайным образом выбирается только одна выборка из набора данных, путь, используемый алгоритмом для достижения минимумов, обычно более шумный, чем ваш типичный алгоритм градиентного спуска. Но это не так уж важно, потому что путь, пройденный алгоритмом, не имеет значения, пока мы достигаем минимумов и со значительно более коротким временем обучения.

Путь, пройденный пакетным градиентным спуском -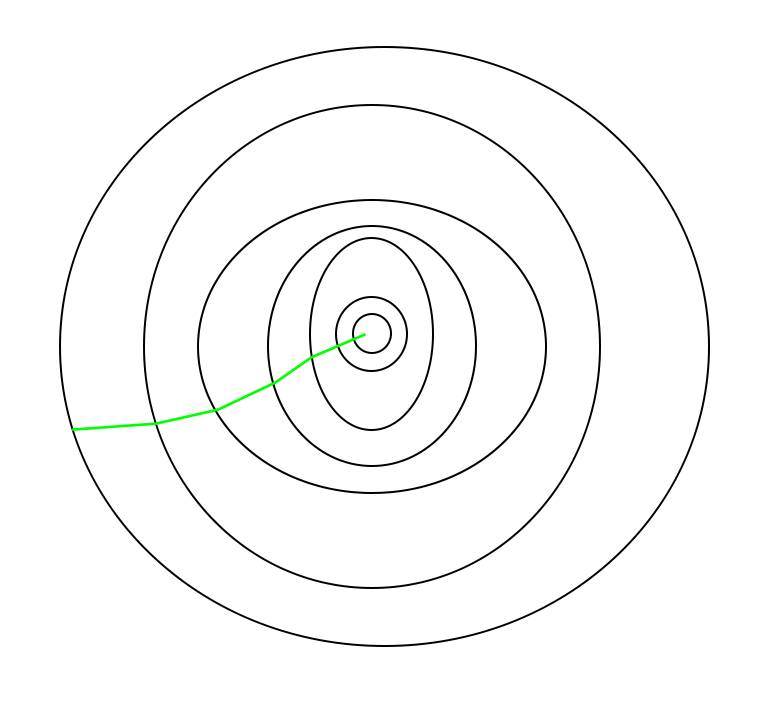

Путь, выбранный стохастическим градиентным спуском -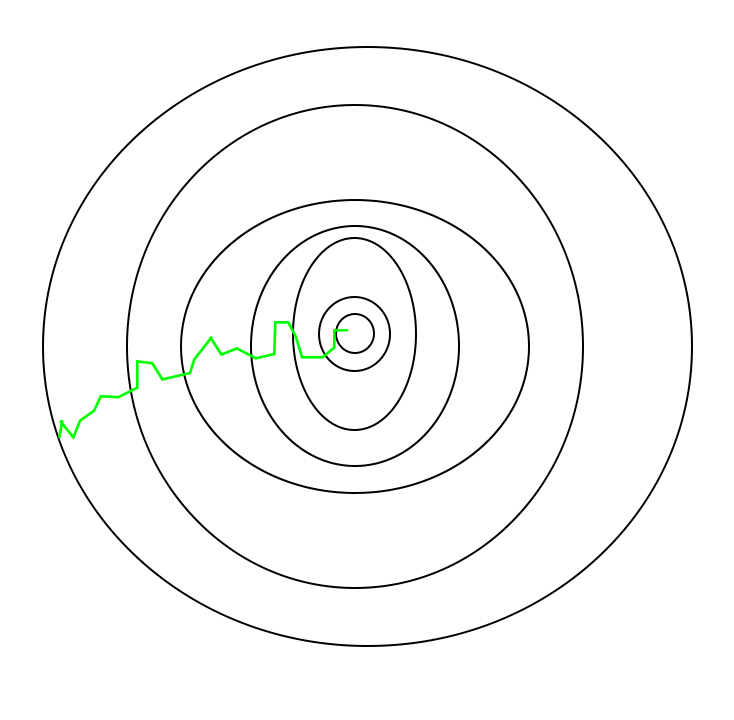

Следует отметить, что, поскольку SGD обычно более шумный, чем типичный градиентный спуск, обычно требуется большее количество итераций для достижения минимумов из-за его случайности в спуске. Несмотря на то, что для достижения минимумов требуется большее количество итераций, чем при обычном градиентном спуске, он все же в вычислительном отношении намного дешевле, чем типичный градиентный спуск. Следовательно, в большинстве сценариев SGD предпочтительнее пакетного градиентного спуска для оптимизации алгоритма обучения.

Псевдокод для SGD на Python:

 def SGD(f, theta0, alpha, num_iters):
    """
       Arguments:
       f -- the function to optimize, it takes a single argument
            and yield two outputs, a cost and the gradient
            with respect to the arguments
       theta0 -- the initial point to start SGD from
       num_iters -- total iterations to run SGD for
       Return:
       theta -- the parameter value after SGD finishes
    """
    start_iter = 0
    theta = theta0
    for iter in xrange (start_iter + 1 , num_iters + 1 ):
        _, grad = f(theta)
  
        # there is NO dot product ! return theta
        theta = theta - (alpha * grad) 

Этот цикл получения значений и их корректировки на основе различных параметров для уменьшения функции потерь называется обратным распространением .

Машинное обучение Продвинутая компьютерная тематика

ML | Стохастический градиентный спуск (SGD)

Стохастический градиентный спуск (SGD):

РЕКОМЕНДУЕМЫЕ СТАТЬИ