ML | Множественная линейная регрессия с использованием Python
Линейная регрессия:
Это основной и часто используемый тип для прогнозного анализа. Это статистический подход к моделированию взаимосвязи между зависимой переменной и заданным набором независимых переменных.
Они бывают двух типов:
- Простая линейная регрессия
- Множественная линейная регрессия
Давайте обсудим множественную линейную регрессию с использованием Python.
Множественная линейная регрессия пытается смоделировать взаимосвязь между двумя или более функциями и откликом путем подбора линейного уравнения к наблюдаемым данным. Шаги по выполнению множественной линейной регрессии почти аналогичны шагам простой линейной регрессии. Разница заключается в оценке. Мы можем использовать его, чтобы узнать, какой фактор имеет наибольшее влияние на прогнозируемый результат, и теперь разные переменные связаны друг с другом.
Here : Y = b0 + b1 * x1 + b2 * x2 + b3 * x3 + …… bn * xn
Y = Dependent variable and x1, x2, x3, …… xn = multiple independent variables
Предположение регрессионной модели:
- Линейность: отношения между зависимыми и независимыми переменными должны быть линейными.
- Гомоскедастичность: следует поддерживать постоянный разброс ошибок.
- Многомерная нормальность: множественная регрессия предполагает, что остатки распределены нормально.
- Отсутствие мультиколлинеарности: предполагается, что мультиколлинеарность данных незначительна или отсутствует.
Фиктивная переменная -
Как мы знаем, в модели множественной регрессии мы используем много категориальных данных. Использование категориальных данных - хороший метод для включения нечисловых данных в соответствующую модель регрессии. Категориальные данные относятся к значениям данных, которые представляют значения категорий-данных с фиксированным и неупорядоченным количеством значений, например, пол (мужской / женский). В регрессионной модели эти значения могут быть представлены фиктивными переменными.
Эти переменные состоят из таких значений, как 0 или 1, представляющих наличие и отсутствие категориального значения.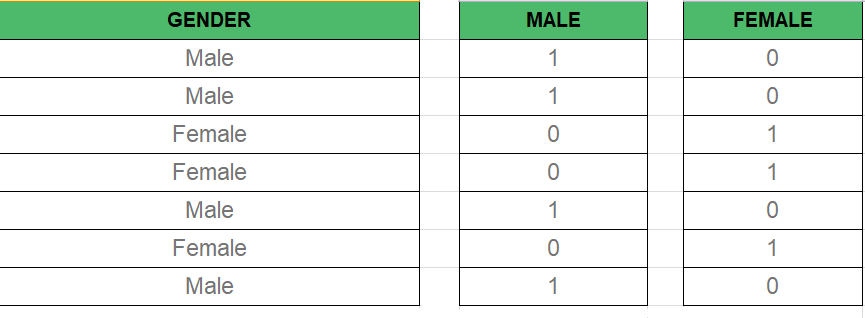
Ловушка фиктивной переменной -
Ловушка фиктивной переменной - это состояние, при котором две или более сильно коррелированы. Проще говоря, мы можем сказать, что одна переменная может быть предсказана на основе предсказания другой. Решение ловушки фиктивной переменной состоит в том, чтобы отбросить одну категориальную переменную. Итак, если есть m фиктивных переменных, тогда в модели используются m-1 переменные.
D2 = D1-1 Здесь D2, D1 = фиктивные переменные
Метод построения моделей:
- Все в
- Обратное исключение
- Прямой выбор
- Двунаправленное исключение
- Сравнение оценок
Обратное исключение:
Шаг № 1: Выберите значительный уровень для начала в модели.
Шаг № 2: Подобрать полную модель со всеми возможными предикторами.
Шаг № 3: Рассмотрите предиктор с самым высоким P-значением. Если P> SL переходите к ШАГУ 4, в противном случае модель готова.
Шаг №4: Удалите предсказатель.
Шаг № 5: Подберите модель без этой переменной.
Прямой выбор:
Шаг № 1: Выберите уровень значимости для входа в модель (например, SL = 0,05)
Шаг № 2: Подобрать все простые регрессионные модели y ~ x (n). Выберите тот, у которого наименьшее значение Р.
Шаг № 3: Сохраните эту переменную и подгоните все возможные модели с одним дополнительным предиктором, добавленным к уже имеющимся.
Шаг №4: Рассмотрите предиктор с наименьшим P-значением. Если P <SL, переходите к шагу №3, в противном случае модель готова.
Шаги, включенные в любую модель множественной линейной регрессии
Шаг № 1: предварительная обработка данных
- Импорт библиотек.
- Импорт набора данных.
- Кодирование категориальных данных.
- Как избежать ловушки фиктивной переменной.
- Разделение набора данных на обучающий набор и тестовый набор.
Шаг # 2: подгонка множественной линейной регрессии к обучающей выборке
Шаг № 3: Прогнозирование результатов набора тестов.
Код 1:
import numpy as npimport matplotlib as mplfrom mpl_toolkits.mplot3d import Axes3Dimport matplotlib.pyplot as plt def generate_dataset(n): x = [] y = [] random_x1 = np.random.rand() random_x2 = np.random.rand() for i in range (n): x1 = i x2 = i / 2 + np.random.rand() * n x.append([ 1 , x1, x2]) y.append(random_x1 * x1 + random_x2 * x2 + 1 ) return np.array(x), np.array(y) x, y = generate_dataset( 200 ) mpl.rcParams[ 'legend.fontsize' ] = 12 fig = plt.figure()ax = fig.gca(projection = '3d' ) ax.scatter(x[:, 1 ], x[:, 2 ], y, label = 'y' , s = 5 )ax.legend()ax.view_init( 45 , 0 ) plt.show() |
Выход: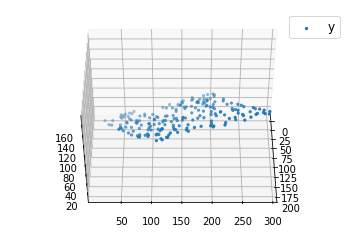
Код 2:
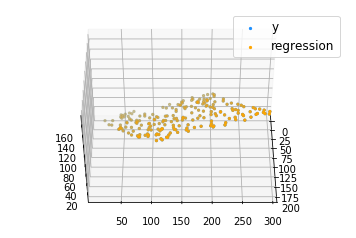
def mse(coef, x, y): return np.mean((np.dot(x, coef) - y) * * 2 ) / 2 def gradients(coef, x, y): return np.mean(x.transpose() * (np.dot(x, coef) - y), axis = 1 ) def multilinear_regression(coef, x, y, lr, b1 = 0.9 , b2 = 0.999 , epsilon = 1e - 8 ): prev_error = 0 m_coef = np.zeros(coef.shape) v_coef = np.zeros(coef.shape) moment_m_coef = np.zeros(coef.shape) moment_v_coef = np.zeros(coef.shape) t = 0 while True : error = mse(coef, x, y) if abs (error - prev_error) < = epsilon: break prev_error = error grad = gradients(coef, x, y) t + = 1 m_coef = b1 * m_coef + ( 1 - b1) * grad v_coef = b2 * v_coef + ( 1 - b2) * grad * * 2 moment_m_coef = m_coef / ( 1 - b1 * * t) moment_v_coef = v_coef / ( 1 - b2 * * t) delta = ((lr / moment_v_coef * * 0.5 + 1e - 8 ) * (b1 * moment_m_coef + ( 1 - b1) * grad / ( 1 - b1 * * t))) coef = np.subtract(coef, delta) coef return coef = np.array([ 0 , 0 , 0 ])c = multilinear_regression(coef, x, y, 1e - 1 )fig = plt.figure()ax = fig.gca(projection = '3d' ) ax.scatter(x[:, 1 ], x[:, 2 ], y, label = 'y' , s = 5 , color = "dodgerblue" ) ax.scatter(x[:, 1 ], x[:, 2 ], c[ 0 ] + c[ 1 ] * x[:, 1 ] + c[ 2 ] * x[:, 2 ], label = 'regression' , s = 5 , color = "orange" ) ax.view_init( 45 , 0 )ax.legend()plt.show() |
Выход: