Минимальное расстояние от точки до сегмента линии с использованием векторов
Даны координаты двух конечных точек A (x1, y1) , B (x2, y2) отрезка прямой и координаты точки E (x, y) ; задача - найти минимальное расстояние от точки до отрезка, образованного с заданными координатами.
Обратите внимание, что оба конца линии могут уходить в бесконечность, т.е. линия не имеет конечных точек. С другой стороны, линейный сегмент имеет начальную и конечную точки, благодаря которым длина линейного сегмента является фиксированной.
Примеры:
Input: A = {0, 0}, B = {2, 0}, E = {4, 0}
Output: 2
To find the distance, dot product has to be found between vectors AB, BE and AB, AE.
AB = (x2 – x1, y2 – y1) = (2 – 0, 0 – 0) = (2, 0)
BE = (x – x2, y – y2) = (4 – 2, 0 – 0) = (2, 0)
AE = (x – x1, y – y1) = (4 – 0, 0 – 0) = (4, 0)
AB . BE = (ABx * BEx + ABy * BEy) = (2 * 2 + 0 * 0) = 4
AB . AE = (ABx * AEx + ABy * AEy) = (2 * 4 + 0 * 0) = 8
Therefore, nearest point from E to line segment is point B.
Minimum Distance = BE =
= 2
Input: A = {0, 0}, B = {2, 0}, E = {1, 1}
Output: 1
Подход: идея состоит в том, чтобы использовать концепцию векторов для решения проблемы, поскольку ближайшая точка всегда лежит на отрезке линии. Предполагая, что вектор AB направлен от A к B, возникают три случая:
1. Ближайшей точкой от точки E на отрезке AB является сама точка B , если скалярное произведение вектора AB (от A до B) и вектора BE (от B до E) положительно, где E - заданная точка. Поскольку AB. BE> 0 , данная точка лежит в том же направлении, что и вектор AB, и ближайшая точка должна быть самой B, потому что ближайшая точка лежит на отрезке прямой.
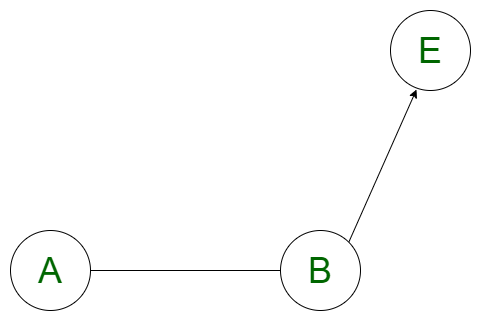
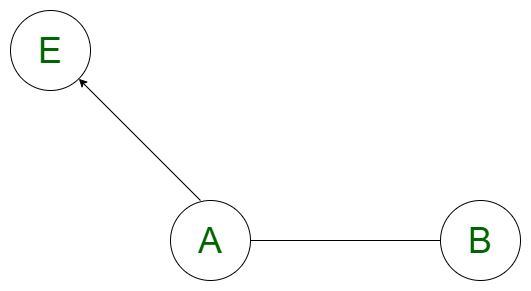
2. Ближайшей точкой от точки E на отрезке AB является сама точка A , если скалярное произведение вектора AB (от A до B) и вектора BE (от B до E) отрицательно, где E - заданная точка. Поскольку AB. BE <0 , данная точка лежит в направлении, противоположном направлению отрезка AB, и ближайшая точка должна быть самой A, потому что ближайшая точка лежит на отрезке прямой.
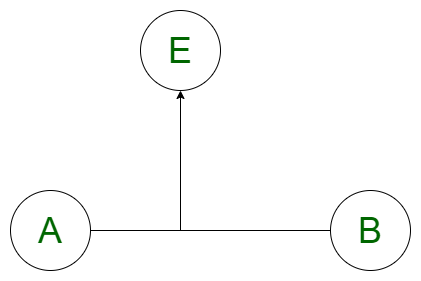
3. Если скалярное произведение равно 0, то точка E перпендикулярна отрезку AB, а расстояние по перпендикуляру к данной точке E от отрезка AB является кратчайшим расстоянием. Если некоторая произвольная точка F является точкой на отрезке, перпендикулярном E, то перпендикулярное расстояние можно вычислить как | EF | = | (AB X AE) / | AB ||
Ниже представлена реализация описанного выше подхода:
C ++
// C++ implementation of the approach#include <bits/stdc++.h>// To store the point#define Point pair<double, double>#define F first#define S secondusing namespace std;// Function to return the minimum distance// between a line segment AB and a point Edouble minDistance(Point A, Point B, Point E){ // vector AB pair< double , double > AB; AB.F = BF - AF; AB.S = BS - AS; // vector BP pair< double , double > BE; BE.F = EF - BF; BE.S = ES - BS; // vector AP pair< double , double > AE; AE.F = EF - AF, AE.S = ES - AS; // Variables to store dot product double AB_BE, AB_AE; // Calculating the dot product AB_BE = (AB.F * BE.F + AB.S * BE.S); AB_AE = (AB.F * AE.F + AB.S * AE.S); // Minimum distance from // point E to the line segment double reqAns = 0; // Case 1 if (AB_BE > 0) { // Finding the magnitude double y = ES - BS; double x = EF - BF; reqAns = sqrt (x * x + y * y); } // Case 2 else if (AB_AE < 0) { double y = ES - AS; double x = EF - AF; reqAns = sqrt (x * x + y * y); } // Case 3 else { // Finding the perpendicular distance double x1 = AB.F; double y1 = AB.S; double x2 = AE.F; double y2 = AE.S; double mod = sqrt (x1 * x1 + y1 * y1); reqAns = abs (x1 * y2 - y1 * x2) / mod; } return reqAns;}// Driver codeint main(){ Point A = make_pair(0, 0); Point B = make_pair(2, 0); Point E = make_pair(1, 1); cout << minDistance(A, B, E); return 0;} |
Джава
// Java implementation of the approachclass GFG{static pair class{ double F, S; public pair( double F, double S) { this .F = F; this .S = S; } public pair() { }}// Function to return the minimum distance// between a line segment AB and a point Estatic double minDistance(pair A, pair B, pair E){ // vector AB pair AB = new pair(); AB.F = BF - AF; AB.S = BS - AS; // vector BP pair BE = new pair(); BE.F = EF - BF; BE.S = ES - BS; // vector AP pair AE = new pair(); AE.F = EF - AF; AE.S = ES - AS; // Variables to store dot product double AB_BE, AB_AE; // Calculating the dot product AB_BE = (AB.F * BE.F + AB.S * BE.S); AB_AE = (AB.F * AE.F + AB.S * AE.S); // Minimum distance from // point E to the line segment double reqAns = 0 ; // Case 1 if (AB_BE > 0 ) { // Finding the magnitude double y = ES - BS; double x = EF - BF; reqAns = Math.sqrt(x * x + y * y); } // Case 2 else if (AB_AE < 0 ) { double y = ES - AS; double x = EF - AF; reqAns = Math.sqrt(x * x + y * y); } // Case 3 else { // Finding the perpendicular distance double x1 = AB.F; double y1 = AB.S; double x2 = AE.F; double y2 = AE.S; double mod = Math.sqrt(x1 * x1 + y1 * y1); reqAns = Math.abs(x1 * y2 - y1 * x2) / mod; } return reqAns;}// Driver codepublic static void main(String[] args){ pair A = new pair( 0 , 0 ); pair B = new pair( 2 , 0 ); pair E = new pair( 1 , 1 ); System.out.print(( int )minDistance(A, B, E));}}// This code is contributed by 29AjayKumar |
Python3
# Python3 implementation of the approachfrom math import sqrt# Function to return the minimum distance# between a line segment AB and a point Edef minDistance(A, B, E) : # vector AB AB = [ None , None ]; AB[ 0 ] = B[ 0 ] - A[ 0 ]; AB[ 1 ] = B[ 1 ] - A[ 1 ]; # vector BP BE = [ None , None ]; BE[ 0 ] = E[ 0 ] - B[ 0 ]; BE[ 1 ] = E[ 1 ] - B[ 1 ]; # vector AP AE = [ None , None ]; AE[ 0 ] = E[ 0 ] - A[ 0 ]; AE[ 1 ] = E[ 1 ] - A[ 1 ]; # Variables to store dot product # Calculating the dot product AB_BE = AB[ 0 ] * BE[ 0 ] + AB[ 1 ] * BE[ 1 ]; AB_AE = AB[ 0 ] * AE[ 0 ] + AB[ 1 ] * AE[ 1 ]; # Minimum distance from # point E to the line segment reqAns = 0 ; # Case 1 if (AB_BE > 0 ) : # Finding the magnitude y = E[ 1 ] - B[ 1 ]; x = E[ 0 ] - B[ 0 ]; reqAns = sqrt(x * x + y * y); # Case 2 elif (AB_AE < 0 ) : y = E[ 1 ] - A[ 1 ]; x = E[ 0 ] - A[ 0 ]; reqAns = sqrt(x * x + y * y); # Case 3 else : # Finding the perpendicular distance x1 = AB[ 0 ]; y1 = AB[ 1 ]; x2 = AE[ 0 ]; y2 = AE[ 1 ]; mod = sqrt(x1 * x1 + y1 * y1); reqAns = abs (x1 * y2 - y1 * x2) / mod; return reqAns;# Driver codeif __name__ = = "__main__" : A = [ 0 , 0 ]; B = [ 2 , 0 ]; E = [ 1 , 1 ]; print (minDistance(A, B, E));# This code is contributed by AnkitRai01 |
C #
// C# implementation of the approachusing System;class GFG{pair class{ public double F, S; public pair( double F, double S) { this .F = F; this .S = S; } public pair() { }}// Function to return the minimum distance// between a line segment AB and a point Estatic double minDistance(pair A, pair B, pair E){ // vector AB pair AB = new pair(); AB.F = BF - AF; AB.S = BS - AS; // vector BP pair BE = new pair(); BE.F = EF - BF; BE.S = ES - BS; // vector AP pair AE = new pair(); AE.F = EF - AF; AE.S = ES - AS; // Variables to store dot product double AB_BE, AB_AE; // Calculating the dot product AB_BE = (AB.F * BE.F + AB.S * BE.S); AB_AE = (AB.F * AE.F + AB.S * AE.S); // Minimum distance from // point E to the line segment double reqAns = 0; // Case 1 if (AB_BE > 0) { // Finding the magnitude double y = ES - BS; double x = EF - BF; reqAns = Math.Sqrt(x * x + y * y); } // Case 2 else if (AB_AE < 0) { double y = ES - AS; double x = EF - AF; reqAns = Math.Sqrt(x * x + y * y); } // Case 3 else { // Finding the perpendicular distance double x1 = AB.F; double y1 = AB.S; double x2 = AE.F; double y2 = AE.S; double mod = Math.Sqrt(x1 * x1 + y1 * y1); reqAns = Math.Abs(x1 * y2 - y1 * x2) / mod; } return reqAns;}// Driver codepublic static void Main(String[] args){ pair A = new pair(0, 0); pair B = new pair(2, 0); pair E = new pair(1, 1); Console.Write(( int )minDistance(A, B, E));}}// This code is contributed by 29AjayKumar |
Javascript
<script>// JavaScript implementation of the approach// Function to return the minimum distance// between a line segment AB and a point Efunction minDistance( A, B, E){ // vector AB var AB=[]; AB.push (B[0] - A[0]); AB.push(B[1] - A[1]); // vector BP var BE=[]; BE.push(E[0] - B[0]); BE.push(E[1] - B[1]); // vector AP var AE=[]; AE.push(E[0] - A[0]), AE.push(E[1] - A[1]); // Variables to store dot product var AB_BE, AB_AE; // Calculating the dot product AB_BE=(AB[0] * BE[0] + AB[1] * BE[1]); AB_AE=(AB[0] * AE[0] + AB[1] * AE[1]); // Minimum distance from // point E to the line segment var reqAns = 0; // Case 1 if (AB_BE > 0) { // Finding the magnitude var y = E[1] - B[1]; var x = E[0] - B[0]; reqAns = Math.sqrt(x * x + y * y); } // Case 2 else if (AB_AE < 0) { var y = E[1] - A[1]; var x = E[0] - A[0]; reqAns = Math.sqrt(x * x + y * y); } // Case 3 else { // Finding the perpendicular distance var x1 = AB[0]; var y1 = AB[1]; var x2 = AE[0]; var y2 = AE[1]; var mod = Math.sqrt(x1 * x1 + y1 * y1); reqAns = Math.abs(x1 * y2 - y1 * x2) / mod; } return reqAns;}var A =[0, 0]; var B = [2, 0]; var E = [1, 1]; document.write( minDistance(A, B, E)); </script> |
1
Сложность времени: O (1)
Вспомогательное пространство: O (1)
Вниманию читателя! Не прекращайте учиться сейчас. Получите все важные математические концепции для соревновательного программирования с курсом Essential Maths for CP по доступной для студентов цене. Чтобы завершить подготовку от изучения языка к DS Algo и многому другому, см. Полный курс подготовки к собеседованию .