Максимальное количество баллов для заполнения матрицы, когда оценка шага представляет собой количество смежных заполненных ячеек

Даны два целых числа N и M , которые обозначают количество строк и столбцов матрицы, которая изначально пуста, задача состоит в том, чтобы заполнить все пустые ячейки и найти максимальное количество очков при их заполнении, когда количество очков для заполнения ячейки такое же, как и количество соседних заполненных ячеек.

Примеры:

Input: N=2, M=3
Output: 7
Explanation:  Matrix after applying 3 operations:

Matrix after applying three operations

Till 3 operations sum is zero. Because each cell having 1 as element has no adjacent cell having element 1. Matrix after 3 more operations:

Matrix in 4th, 5th and 6th operation

4th Cell has element 1 in red color has 2 adjacent cells(up and right) having 1 . Score till here is 2.
2nd Cell has element 1 in blue color has 3 adjacent cells(left, right, down) having 1. Score till here is 2+3=5.
6th Cell has element 1 in Orange color has 2 adjacent cells(left, up) having 1. Score till here is 5+2=7.
Hence, Total maximum score that can obtain is 7.

Input: N = 5, M = 7
Output: 58

Подход: Задача может быть решена на основе следующей идеи:

Put 1 on cells of matrix in such a way that that it looks like chessboard of elements 1 and empty cells. Then just put 1 at empty cells and count adjacent cell having 1. For more clarification, See the illustration of approach below.

Иллюстрация подхода:

 If N = 4, M = 4

initially Matrix will be:

Initial matrix

For making chessboard like pattern of 1, Both the index of matrix should be odd or even. On traversing process on matrix we will skip these cells, Because they are not contributing in increasing score. After applying 8 operations and making matrix like chessboard of element 1:

Matrix applying 8 operations(from 1 to 8)

Now,  make 8 more operations one by one, put 1 at empty cells of matrix and count number of adjacent elements while putting 1 in each of these operations.

In image below next 8 operations are shown and adjacent cells are showed by arrows.

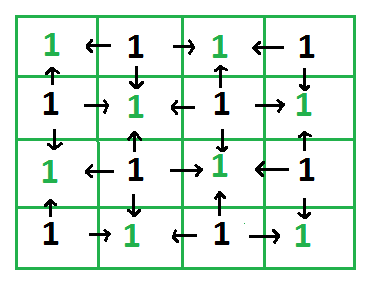
matrix after applying more 8 operations(from 9 to 16)

 In the image above, 8 black 1s are put one by one in operations from 9 to 16 and adjacent cells are represented by arrows. Formally, Each arrow can be considered as 1 score, There are total 24 arrows. Hence 4*4 matrix will have maximum possible score as 24, in exactly 16 operations.

Observations

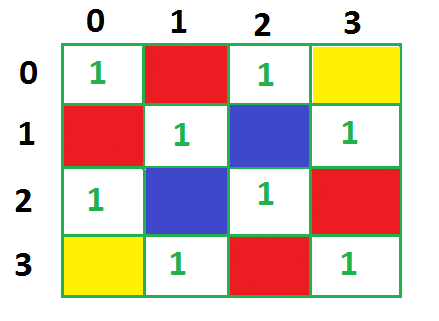
From the above image it can be seen,

• If the empty cell is at any corner suppose (yellow color in above picture) then it will contribute 2 to total score.
• Those cells which are at borders (red cells) will contribute 3 to total score
• Rest of the cell (blue colored) will contribute 4 in total score.

Выполните следующие шаги для применения подхода грубой силы.

• Перемещайтесь по матрице, используя два вложенных цикла.
• Если оба индекса нечетные или четные, то пропустите эти ячейки матрицы.
• Инициализируйте переменную total_sum и добавьте 2, 3 или 4 к total_sum , проверив, что пустая ячейка находится в углу, на границе или в другом месте, чем эти два, используя описанный выше подход.
• Вывести значение total_sum .

Ниже приведена реализация описанного выше подхода.

Временная сложность: O(N*M)
Вспомогательное пространство: O(1)

Оптимизированный подход: можно заметить, что общий возможный балл можно получить, используя формулу:

If we create a chessboard pattern, for each row, there can be at most (M-1) pairs of adjacent cells where the values of both the cells are different. Each such pair will contribute 1 point to the final score.
So contribution from each row is (M-1). Therefore, contribution by all rows is N*(M-1).

Similary, each column can make (N-1) pairs of adjacent cells with different values. So total contribution by all the columns will be M*(N-1).

Therefore the total possible maximum score is N*(M-1) + M*(N-1).

Временная сложность: O(1)
Вспомогательное пространство: O(1)