LIS с использованием дерева сегментов

Опубликовано: 2 Марта, 2022

Вам дан массив целых чисел, вам нужно найти длину самой длинной возрастающей подпоследовательности.

Для решения проблемы может быть 4 подхода.

1) Грубая сила:
В этом подходе мы пытаемся найти все возрастающие подпоследовательности, а затем возвращаем максимальную длину самой длинной возрастающей подпоследовательности. Для этого мы используем рекурсивную функцию, которая возвращает длину LIS, возможную от текущего элемента и далее.
Сложность времени: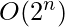
Космическая сложность: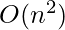

2) динамическое программирование
Этот подход основан на том факте, что LIS до i-го индекса не зависит от последующих (n-i + 1) элементов. Кроме того, LIS до (i + 1) -го элемента может быть вычислен путем проверки LIS, полученного от индекса 0 до i.
Подход динамического программирования
Сложность времени: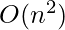
Космическая сложность: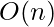

3) Использование двоичного поиска
Элементы хранятся в возрастающем порядке в массиве DP, где индекс определяется с помощью двоичного поиска. Длина массива дает длину LIS.
Сложность времени: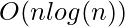
Космическая сложность: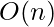
Пожалуйста, обратитесь к разделу Построение самой длинной возрастающей подпоследовательности (N log N) для получения подробной информации.

4) Использование дерева сегментов
Элементы сначала сортируются в порядке возрастания с сохранением их исходных индексов. Для строго увеличивающейся LIS для равных элементов элемент с более высоким индексом получает более раннюю позицию, чем более низкий. Это может быть сохранено в массиве пар.
Теперь они заполнены в дереве сегментов. В соответствии с их положением в отсортированном массиве они заполняются в дереве сегментов в листьях, соответствующих их исходным индексам.
Первоначально дерево сегментов было инициализировано нулями. Теперь предположим, что мы обработали i-й элемент в отсортированном массиве. На (i + 1) -й итерации пусть исходная позиция значения равна j.
Затем он заполнит j-й лист в дереве сегментов, значение которого будет максимальным значением листьев от 0 до (j-1) +1.
(Длина LIS, образованного элементами, меньшими, чем в предшествующем подмассиве, и +1 для его включения)
Arr [] = {5, 1, 3, 9} Индексы: {0, 1, 2, 3}
Sorted_Arr [] = {1, 3, 5, 9} Original_Indices: {1, 2, 0, 3} Индексы: {0, 1, 2, 3}

C++

// Finding the Longest Increasing Subsequence using
// Segment Tree
#include <bits/stdc++.h>
using namespace std;
 
// function to compare two pairs
int compare(pair<int, int> p1, pair<int, int> p2)
{
     /* For same values, element with the higher
        index appear earlier in the sorted array.
        This is for strictly increasing subsequence.
        For increasing subsequence, the lower index
         appears earlier in the sorted array. */
    if (p1.first == p2.first)
        return p1.second > p2.second;
     
    // Sorting the array according to their values.
    return p1.first < p2.first;
}
 
// Building the entire Segment tree, the root of which
// contains the length of the LIS
void buildTree(int* tree, int pos, int low, int high,
                                 int index, int value)
{
    // index is the original index of current element
    // If the index is not present in the given range,
    // then simply return
    if (index < low || index > high)
        return;
 
    // If low == high then the current position should
    // be updated to the value
    if (low == high) {
        tree[pos] = value;
        return;
    }
 
    int mid = (high + low) / 2;
 
    // Recursively call the function on the
    // child nodes
    buildTree(tree, 2 * pos + 1, low, mid, index, value);
    buildTree(tree, 2 * pos + 2, mid + 1, high, index, value);
 
    // Assign the current position the max of the 2 child
    // nodes
    tree[pos] = max(tree[2 * pos + 1], tree[2 * pos + 2]);
}
 
// Function to query the Segment tree and return the
// value for a given range
int findMax(int* tree, int pos, int low, int high,
                               int start, int end)
{
    // Query: Same as the query function of Segment tree
    // If the current range is totally inside the query
    // range, return the value of current position
    if (low >= start && high <= end)
        return tree[pos];
     
    // If it is out of bound, return the minimum which
    // would be 0 in this case
    if (start > high || end < low)
        return 0;   
 
    // Partial overlap
    int mid = (high + low) / 2;
 
    // Call findMax on child nodes recursively and
    // return the maximum of the two
    return max(findMax(tree, 2 * pos + 1, low, mid,
                                        start, end),
               findMax(tree, 2 * pos + 2, mid + 1,
                                high, start, end));
}
 
int findLIS(int arr[], int n)
{
    // The array of pairs stores the integers and
    // indices in p[i]
    pair<int, int> p[n];
    for (int i = 0; i < n; i++) {
        p[i].first = arr[i];
        p[i].second = i;
    }
 
    // Sorting the array in increasing order
    // of the elements
    sort(p, p + n, compare);
 
    // Calculating the length of the segment-tree
    int len = pow(2, (int)(ceil(sqrt(n))) + 1) - 1;
    int tree[len];
 
    // Initializing the tree with zeroes
    memset(tree, 0, sizeof(tree));
 
    // Building the segment-tree, the root node of
    // which contains the length of LIS for the n
    // elements
    for (int i = 0; i < n; i++) {
        buildTree(tree, 0, 0, n - 1, p[i].second,
     findMax(tree, 0, 0, n - 1, 0, p[i].second) + 1);
    }
     
    return tree[0];
}
 
// Driver code
int main()
{
    int arr[] = { 10, 22, 9, 33, 21, 50, 41, 60 };
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << "Length of the LIS: " << findLIS(arr, n);
    return 0;
}

Java

// Finding the Longest Increasing Subsequence
// using Segment Tree
import java.io.*;
import java.util.*;
 
class Pair
{
    int first;
    int second;
}
 
class GFG{
 
// Building the entire Segment tree, the root of which
// contains the length of the LIS
static void buildTree(int[] tree, int pos, int low,
                      int high, int index, int value)
{
     
    // Index is the original index of current element
    // If the index is not present in the given range,
    // then simply return
    if (index < low || index > high)
        return;
 
    // If low == high then the current position
    // should be updated to the value
    if (low == high)
    {
        tree[pos] = value;
        return;
    }
 
    int mid = (high + low) / 2;
 
    // Recursively call the function on the
    // child nodes
    buildTree(tree, 2 * pos + 1, low, mid,
              index, value);
    buildTree(tree, 2 * pos + 2, mid + 1, high,
              index, value);
 
    // Assign the current position the max of
    // the 2 child nodes
    tree[pos] = Math.max(tree[2 * pos + 1],
                         tree[2 * pos + 2]);
}
 
// Function to query the Segment tree and
// return the value for a given range
static int findMax(int[] tree, int pos, int low,
                   int high, int start, int end)
{
     
    // Query: Same as the query function of Segment
    // tree. If the current range is totally inside
    // the query range, return the value of current
    // position
    if (low >= start && high <= end)
        return tree[pos];
 
    // If it is out of bound, return the minimum
    // which would be 0 in this case
    if (start > high || end < low)
        return 0;
 
    // Partial overlap
    int mid = (high + low) / 2;
 
    // Call findMax on child nodes recursively
    // and return the maximum of the two
    return Math.max(findMax(tree, 2 * pos + 1, low, mid,
                            start, end),
                    findMax(tree, 2 * pos + 2, mid + 1,
                            high, start, end));
}
 
static int findLIS(int arr[], int n)
{
     
    // The array of pairs stores the integers
    // and indices in p[i]
    List<Pair> p = new ArrayList<Pair>();
 
    for(int i = 0; i < n; i++)
    {
        Pair p1 = new Pair();
        p1.first = arr[i];
        p1.second = i;
        p.add(p1);
    }
 
    // Sorting the array in increasing order
    // of the elements
    Collections.sort(p, (p1, p2) ->
    {
         
        /* For same values, element with the higher
           index appear earlier in the sorted array.
           This is for strictly increasing subsequence.
           For increasing subsequence, the lower index
            appears earlier in the sorted array. */
        if (p1.first == p2.first)
            return p2.second - p1.second;
 
        // Sorting the array according to their values.
        return p1.first - p2.first;
    });
 
    // Calculating the length of the segment-tree
    int len = (int)(Math.pow(
              2, (int)(Math.ceil(Math.sqrt(n))) + 1)) - 1;
    int[] tree = new int[len];
 
    // Building the segment-tree, the root node of
    // which contains the length of LIS for the n
    // elements
    for(int i = 0; i < n; i++)
    {
        buildTree(tree, 0, 0, n - 1, p.get(i).second,
                  findMax(tree, 0, 0, n - 1, 0,
                          p.get(i).second) + 1);
    }
    return tree[0];
}
 
// Driver Code
public static void main(String[] args)
{
    int arr[] = { 10, 22, 9, 33, 21, 50, 41, 60 };
    int n = arr.length;
     
    System.out.println("Length of the LIS: " +
                       findLIS(arr, n));
}
}
 
// This code is contributed by jithin

Length of the LIS: 5

Сложность времени: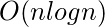

Космическая сложность: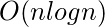

Эта статья предоставлена Притамом Патхаком. Если вам нравится GeeksforGeeks, и вы хотели бы внести свой вклад, вы также можете написать статью с помощью provide.geeksforgeeks.org или отправить ее по электронной почте на deposit@geeksforgeeks.org. Посмотрите, как ваша статья появляется на главной странице GeeksforGeeks, и помогите другим гикам.
Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсужденной выше.

Продвинутая компьютерная тематика

LIS с использованием дерева сегментов

C++

Java

РЕКОМЕНДУЕМЫЕ СТАТЬИ