Косинусное подобие

Предварительное условие - Измерение расстояния в интеллектуальном анализе данных

В интеллектуальном анализе данных мера сходства относится к расстоянию с измерениями, представляющими особенности объекта данных в наборе данных. Если это расстояние меньше, будет высокая степень подобия, но когда расстояние большое, будет низкая степень сходства.

Некоторые из популярных мер сходства:

1. Евклидово расстояние.
2. Манхэттенское расстояние.
3. Сходство Жаккара.
4. Расстояние Минковского.
5. Косинусное подобие.

Косинусное сходство - это показатель, помогающий определить, насколько похожи объекты данных независимо от их размера. Мы можем измерить сходство между двумя предложениями в Python, используя косинусное сходство. При косинусном подобии объекты данных в наборе данных обрабатываются как вектор. Формула для определения косинусного сходства между двумя векторами:

 Cos (х, у) = х. у / || х || * || y ||

где,

• Икс . y = произведение (точка) векторов x и y.
• || х || и || y || = длина двух векторов 'x' и 'y'.
• || х || * || y || = перекрестное произведение двух векторов 'x' и 'y'.

Пример :
Рассмотрим пример, чтобы найти сходство между двумя векторами - 'x' и 'y' , используя косинусное сходство.

Вектор 'x' имеет значения, x = {3, 2, 0, 5}
Вектор y имеет значения, y = {1, 0, 0, 0}

Формула для вычисления косинусного подобия: Cos (x, y) = x. у / || х || * || и ||

 Икс. у = 3 * 1 + 2 * 0 + 0 * 0 + 5 * 0 = 3

|| х || = √ (3) ^ 2 + (2) ^ 2 + (0) ^ 2 + (5) ^ 2 = 6,16

|| и || = √ (1) ^ 2 + (0) ^ 2 + (0) ^ 2 + (0) ^ 2 = 1

∴ Cos (x, y) = 3 / (6,16 * 1) = 0,49

Различие между двумя векторами 'x' и 'y' определяется следующим образом:

 ∴ Dis (x, y) = 1 - Cos (x, y) = 1 - 0,49 = 0,51

• Косинусное сходство между двумя векторами измеряется в 'θ'.
• Если θ = 0 °, векторы «x» и «y» перекрываются, тем самым доказывая, что они подобны.
• Если θ = 90 °, векторы «x» и «y» различны.

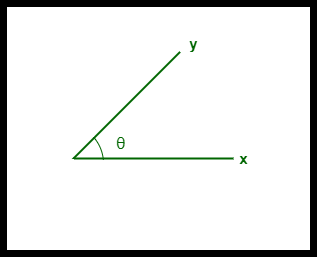
Косинусное сходство между двумя векторами

Преимущества :

• Косинусное сходство полезно, потому что даже если два похожих объекта данных находятся далеко друг от друга на евклидово расстояние из-за размера, они все равно могут иметь меньший угол между ними. Чем меньше угол, тем больше сходство.
• При нанесении на многомерное пространство косинусное подобие фиксирует ориентацию (угол) объектов данных, а не величину.