Корреляционное тестирование Спирмена в программировании на R
Сила связи между двумя переменными известна как тест корреляции. Например, если кто-то интересуется, существует ли связь между весами матери и дочери, для ответа на этот вопрос можно рассчитать коэффициент корреляции. Чтобы узнать больше о корреляции, см. Корреляция.
Методы корреляционного анализа
В основном есть два типа корреляции:
- Параметрическая корреляция - корреляция Пирсона (r): она измеряет линейную зависимость между двумя переменными (x и y) и известна как тест параметрической корреляции, поскольку зависит от распределения данных.
- Непараметрическая корреляция - Кендалл (тау) и Спирмен (ро): это коэффициенты корреляции на основе ранга, известные как непараметрическая корреляция.
Формула корреляции Спирмена
Корреляция Спирмена - это непараметрическая корреляция, также известная как коэффициенты корреляции на основе рангов. Формула для расчета корреляции Спирмена выглядит следующим образом:
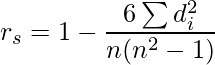
where,
rs: Spearman Correlation coefficient
di: The difference in the ranks given to the two variables values for each item of the data,
n: Total number of observation
Примечание:
- r s принимает значение от -1 (отрицательная ассоциация) до 1 (положительная ассоциация).
- r s = 0 означает, что ассоциации нет.
- Если ассоциация монотонно возрастает, то r s = 1.
- Если ассоциация монотонно убывает, то r s = -1.
- Его можно использовать, когда ассоциация нелинейна.
- Его можно применять для порядковых переменных.
Реализация в R
В языке R есть два метода расчета коэффициента корреляции. Его можно вычислить с помощью функций cor() или cor.test() Можно отметить, что cor() вычисляет коэффициент корреляции, тогда как cor.test() вычисляет тест для ассоциации или корреляции между парными выборками. Он возвращает как коэффициент корреляции, так и уровень значимости (или p-значение) корреляции.
Syntax:
cor(x, y, method = “spearman”)
cor.test(x, y, method = “spearman”)Parameters:
x, y: numeric vectors with the same length
method: correlation method
Пример 1:
# Использование метода cor()
# R program to illustrate# Spearman Correlation Testing# Using cor() # Taking two numeric# Vectors with same lengthx = c( 15 , 18 , 21 , 15 , 21 )y = c( 25 , 25 , 27 , 27 , 27 ) # Calculating# Correlation coefficient# Using cor() methodresult = cor(x, y, method = "spearman" ) # Print the resultcat( "Spearman correlation coefficient is:" , result) |
Выход:
Коэффициент корреляции Спирмена: 0,4564355
# Использование cor.test()
# R program to illustrate# Spearman Correlation Testing# Using cor.test() # Taking two numeric# Vectors with same lengthx = c( 15 , 18 , 21 , 15 , 21 )y = c( 25 , 25 , 27 , 27 , 27 ) # Calculating# Correlation coefficient# Using cor.test() methodresult = cor.test(x, y, method = "spearman" ) # Print the resultprint (result) |
Выход:
Ранговая корреляция Спирмена ро
данные: x и y
S = 10,871, значение p = 0,4397
Альтернативная гипотеза: истинное ро не равно 0
примерные оценки:
ро
0,4564355
В выводе выше:
- S - значение тестовой статистики (S = 10,871)
- p-значение - это уровень значимости тестовой статистики (p-значение = 0,4397).
- Альтернативная гипотеза - это символьная строка, описывающая альтернативную гипотезу (истинное rho не равно 0).
- выборочные оценки - коэффициент корреляции. Для коэффициента корреляции Спирмана он называется ро (Cor.coeff = 0,4564).
Пример 2:
Данные: загрузите файл CSV здесь.
# R program to illustrate# Spearman Correlation Testing # Import data into RStudiodf = read.csv( "Auto.csv" ) # Taking two column# Vectors with same lengthx = df$mpgy = df$weight # Calculating# Correlation coefficient# Using cor() methodresult = cor(x, y, method = "spearman" ) # Print the resultcat( "Spearman correlation coefficient is:" , result) # Using cor.test() methodres = cor.test(x, y, method = "spearman" )print (res) |
Выход:
Коэффициент корреляции Спирмена: -0,9140708
Ранговая корреляция Спирмена ро
данные: x и y
S = 8613223, значение p <2,2e-16
Альтернативная гипотеза: истинное ро не равно 0
примерные оценки:
ро
-0,9140708