Количество инверсий в массиве с использованием сортировки слиянием

Счетчик инверсии для массива указывает – насколько далек (или близок) массив от сортировки. Если массив уже отсортирован, то счетчик инверсии равен 0, но если массив отсортирован в обратном порядке, то счетчик инверсии будет максимальным.

Дан массив a[] . Задача состоит в том, чтобы найти количество инверсий a[] . Где два элемента a[i] и a[j] образуют инверсию, если a[i] > a[j] и i < j.

Примеры:

Input: arr[] = {8, 4, 2, 1}
Output: 6
Explanation: Given array has six inversions: (8, 4), (4, 2), (8, 2), (8, 1), (4, 1), (2, 1).

Input: arr[] = {1, 20, 6, 4, 5}
Output: 5
Explanation: Given array has five inversions: (20, 6), (20, 4), (20, 5), (6, 4), (6, 5). 

Наивный подход:

Traverse through the array, and for every index, find the number of smaller elements on its right side of the array. This can be done using a nested loop. Sum up the counts for all indices in the array and print the sum.

Выполните следующие шаги, чтобы реализовать идею:

• Пройтись по массиву от начала до конца
• Для каждого элемента найдите количество элементов меньше текущего числа до этого индекса, используя другой цикл.
• Суммируйте количество инверсий для каждого индекса.
• Выведите количество инверсий.

Ниже приведена реализация вышеуказанного подхода:

Временная сложность: O(N ² ). Для обхода массива от начала до конца необходимы два вложенных цикла.
Вспомогательное пространство: O(1), дополнительное пространство не требуется.

Подсчитайте инверсии в массиве с помощью сортировки слиянием:

Ниже представлена идея решения проблемы:

Use Merge sortwith modification that every time an unsorted pair is found increment count by one and return count at the end.

Иллюстрация:

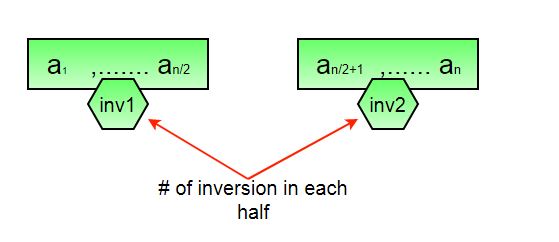
Suppose the number of inversions in the left half and right half of the array (let be inv1 and inv2); what kinds of inversions are not accounted for in Inv1 + Inv2? The answer is – the inversions that need to be counted during the merge step. Therefore, to get the total number of inversions that needs to be added are the number of inversions in the left subarray, right subarray, and merge().

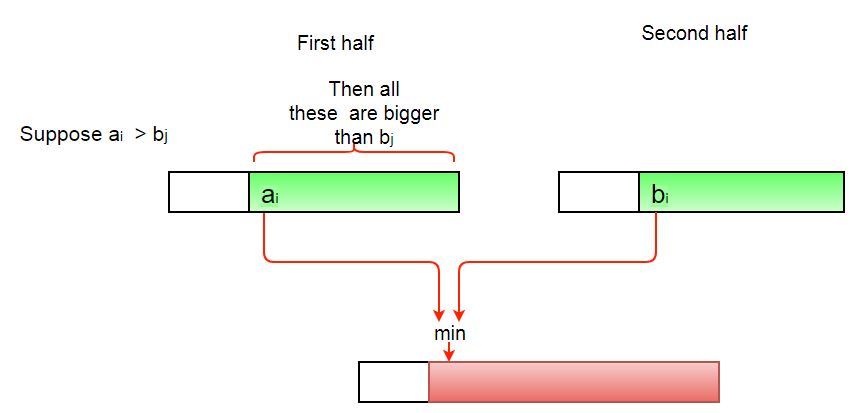
How to get the number of inversions in merge()? 
In merge process, let i is used for indexing left sub-array and j for right sub-array. At any step in merge(), if a[i] is greater than a[j], then there are (mid – i) inversions. because left and right subarrays are sorted, so all the remaining elements in left-subarray (a[i+1], a[i+2] … a[mid]) will be greater than a[j]

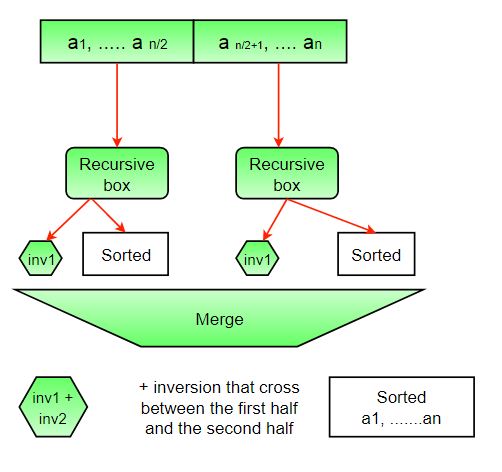
The complete picture:

Выполните следующие шаги, чтобы реализовать идею:

• Идея аналогична сортировке слиянием, разделите массив на две равные или почти равные половины на каждом шаге, пока не будет достигнут базовый случай.
• Создайте функцию слияния, которая подсчитывает количество инверсий при слиянии двух половин массива,
  • Создайте два индекса i и j, i — индекс первой половины, а j — индекс второй половины.
  • Если a[i] больше, чем a[j], то имеются (mid – i) инверсии, потому что левый и правый подмассивы отсортированы, поэтому все оставшиеся элементы в левом подмассиве (a[i+1], a[i +2] … a[mid]) будет больше, чем a[j].
• Создайте рекурсивную функцию, чтобы разделить массив на половины и найти ответ, суммируя количество инверсий в первой половине, количество инверсий во второй половине и количество инверсий путем их слияния.
  • Базовый случай рекурсии - это когда в данной половине есть только один элемент.
• Распечатайте ответ.

Ниже приведена реализация вышеуказанного подхода:

Сложность по времени: O(n * log n). Используемый алгоритм — «разделяй и властвуй», т.е. сортировка слиянием, сложность которой составляет O(n log n).
Вспомогательное пространство: O(n), временный массив.

Примечание. Приведенный выше код изменяет (или сортирует) входной массив. Если мы хотим подсчитывать только инверсии, нам нужно создать копию исходного массива и вызвать функцию mergeSort() для копии, чтобы сохранить исходный порядок массива.

Подсчитайте инверсии в массиве, используя Heapsortand Bisection:

Выполните следующие шаги, чтобы реализовать идею:

• Создайте кучу с новыми парными элементами (элемент, индекс).
• После их сортировки выдвигайте последовательно каждый минимум и создавайте новый отсортированный список с индексами.
• Вычислите разницу между исходным индексом и индексом деления пополам нового отсортированного списка.
• Суммируйте разницу.

Ниже приведена идея реализации вышеуказанного подхода:

Временная сложность: O(n * log n). И пирамидальная сортировка, и деление пополам могут выполнять отсортированную вставку в (log n) в каждом элементе.
Вспомогательное пространство: O(n). Куча и новый список имеют ту же длину, что и исходный массив.

Вам может понравиться:
Подсчет инверсий в массиве | Набор 2 (с использованием самобалансирующегося BST)
Подсчет инверсий с использованием Set в C++ STL
Подсчет инверсий в массиве | Набор 3 (с использованием BIT)
Пожалуйста, пишите комментарии, если вы обнаружите какую-либо ошибку в приведенной выше программе/алгоритме или другие способы ее решения.