Кластеризация DBSCAN в ML | Кластеризация на основе плотности

Опубликовано: 24 Июля, 2021

Кластерный анализ или просто кластеризация - это, по сути, метод обучения без учителя, который делит точки данных на ряд определенных пакетов или групп, так что точки данных в одних и тех же группах имеют схожие свойства, а точки данных в разных группах имеют разные свойства в некотором смысле. Он состоит из множества различных методов, основанных на разной эволюции.
Например, K-средние (расстояние между точками), распространение сродства (расстояние на графике), средний сдвиг (расстояние между точками), DBSCAN (расстояние между ближайшими точками), гауссовские смеси (расстояние Махаланобиса до центров), спектральная кластеризация (расстояние на графике) и т. Д. .

По сути, все методы кластеризации используют один и тот же подход, т.е. сначала мы вычисляем сходства, а затем используем его для кластеризации точек данных в группы или пакеты. Здесь мы сосредоточимся на методе кластеризации приложений на основе пространственной плотности с шумом (DBSCAN).

Кластеры - это плотные области в пространстве данных, разделенные областями с более низкой плотностью точек. Алгоритм DBSCAN основан на этом интуитивном понятии «кластеры» и «шум». Ключевая идея состоит в том, что для каждой точки кластера окрестность заданного радиуса должна содержать как минимум минимальное количество точек.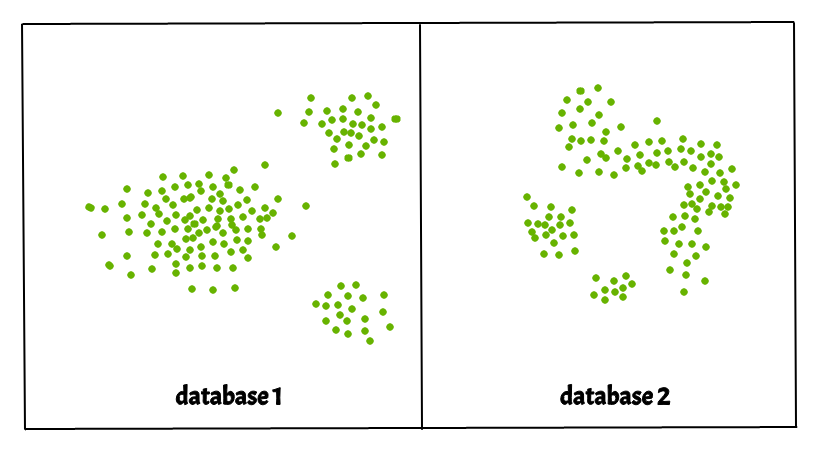

Почему именно DBSCAN?
Методы разделения (K-средних, кластеризация PAM) и иерархическая кластеризация работают для поиска кластеров сферической формы или выпуклых кластеров. Другими словами, они подходят только для компактных и хорошо разделенных кластеров. Более того, на них также сильно влияет наличие шума и выбросов в данных.

Данные из реальной жизни могут содержать неточности, например:
i) Кластеры могут иметь произвольную форму, такую как показано на рисунке ниже.
ii) Данные могут содержать шум.

На рисунке ниже показан набор данных, содержащий невыпуклые кластеры и выбросы / шумы. Учитывая такие данные, алгоритм k-средних имеет трудности с идентификацией этих кластеров произвольной формы.

Алгоритм DBSCAN требует двух параметров -

eps : определяет окрестность вокруг точки данных, т.е. если расстояние между двумя точками меньше или равно eps, то они считаются соседями. Если значение eps выбрано слишком маленьким, большая часть данных будет считаться выбросами. Если он выбран очень большим, кластеры объединятся, и большинство точек данных будут в одних и тех же кластерах. Один из способов найти значение eps основан на графике k-расстояний .
MinPts : минимальное количество соседей (точек данных) в радиусе eps. Чем больше набор данных, тем больше значение MinPts должно быть выбрано. Как правило, минимальное количество MinPts может быть получено из количества измерений D в наборе данных, как, MinPts >= D+1 . Минимальное значение MinPts должно быть выбрано не менее 3.
In this algorithm, we have 3 types of data points.
Core Point: A point is a core point if it has more than MinPts points within eps.
Border Point: A point which has fewer than MinPts within eps but it is in the neighborhood of a core point.
Noise or outlier: A point which is not a core point or border point.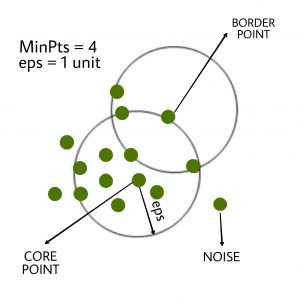

Алгоритм DBSCAN можно абстрагировать, выполнив следующие шаги:

Найдите все соседние точки в пределах eps и определите основные точки или посещенные с более чем соседями MinPts.
Для каждой точки ядра, если она еще не назначена кластеру, создайте новый кластер.
Рекурсивно найдите все точки, связанные с плотностью, и назначьте их тому же кластеру, что и центральная точка.
Точка а и б , как говорят, плотности связаны , если существуют точку с , который имеет достаточное число точек в своих соседях и обеих точках а и б находятся в пределах расстояния EPS. Это цепной процесс. Итак, если b является соседом c , c является соседом d , d является соседом e , который, в свою очередь, является соседом a, подразумевает, что b является соседом a .
Перебрать оставшиеся непосещенные точки в наборе данных. Те точки, которые не принадлежат ни одному кластеру, являются шумом.

Ниже представлен алгоритм кластеризации DBSCAN в псевдокоде:

 DBSCAN (набор данных, eps, MinPts) {
# индекс кластера
С = 1
для каждой непосещенной точки p в наборе данных {
         пометить p как посещенный
         # найти соседей
         Соседи N = найти соседние точки p

         если | N |> = MinPts:
             N = NUN '
             если p 'не является членом какого-либо кластера:
                 добавить p 'в кластер C 
}

Реализация вышеуказанного алгоритма на Python:

Здесь мы будем использовать библиотеку Python sklearn для вычисления DBSCAN. Мы также будем использовать matplotlib.pyplot для визуализации кластеров.

Используемый набор данных можно найти здесь.

 import numpy as np
 from sklearn.cluster import DBSCAN
 from sklearn import metrics
 from sklearn.datasets.samples_generator import make_blobs
 from sklearn.preprocessing import StandardScaler
 from datasets import sklearn
 
# Load data in X
 db = DBSCAN(eps = 0.3 , min_samples = 10 ).fit(X)
 core_samples_mask = np.zeros_like(db.labels_, dtype = bool )
 core_samples_mask[db.core_sample_indices_] = True
 labels = db.labels_
 
# Number of clusters in labels, ignoring noise if present.
 n_clusters_ = len ( set (labels)) - ( 1 if - 1 in labels else 0 )
 
print (labels)
 
# Plot result
 import matplotlib.pyplot as plt
 
# Black removed and is used for noise instead.
 unique_labels = set (labels)
 colors = [ 'y' , 'b' , 'g' , 'r' ]
 print (colors)
 for k, col in zip (unique_labels, colors):
    if k = = - 1 :
        # Black used for noise.
        col = 'k'
 
    class_member_mask = (labels = = k)
 
    xy = X[class_member_mask & core_samples_mask]
    plt.plot(xy[:, 0 ], xy[:, 1 ], 'o' , markerfacecolor = col,
                                      markeredgecolor = 'k' ,
                                      markersize = 6 )
 
    xy = X[class_member_mask & ~core_samples_mask]
    plt.plot(xy[:, 0 ], xy[:, 1 ], 'o' , markerfacecolor = col,
                                      markeredgecolor = 'k' ,
                                      markersize = 6 )
 
plt.title( 'number of clusters: %d' % n_clusters_)
 plt.show()

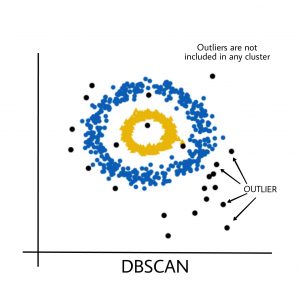
Выход: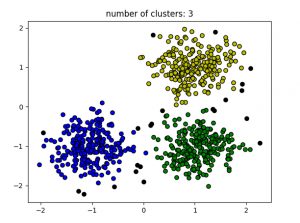

Черные точки представляют собой выбросы. Изменяя eps и MinPts , мы можем изменить конфигурацию кластера.

Теперь следует задать вопрос: почему мы должны использовать DBSCAN, если K-Means является широко используемым методом в кластерном анализе?

Недостаток K-MEANS:

K-Means формирует только сферические кластеры. Этот алгоритм не работает, когда данные не являются сферическими (т. Е. Одинаковая дисперсия во всех направлениях).
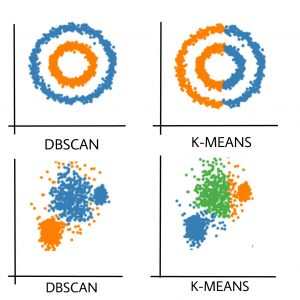
Алгоритм K-средних чувствителен к выбросам. Выбросы могут очень сильно исказить кластеры в K-средних.
Алгоритм K-средних требует указания априорного числа кластеров и т. Д.

По сути, алгоритм DBSCAN преодолевает все вышеупомянутые недостатки алгоритма K-Means. Алгоритм DBSCAN идентифицирует плотную область, группируя точки данных, которые близки друг к другу, на основе измерения расстояния.

Реализацию вышеуказанного алгоритма на Python без использования библиотеки sklearn можно найти здесь dbscan_in_python.

Рекомендации :
https://en.wikipedia.org/wiki/DBSCAN
https://scikit-learn.org/stable/auto_examples/cluster/plot_dbscan.html

Внимание компьютерщик! Укрепите свои основы с помощью базового курса программирования Python и изучите основы.

Для начала подготовьтесь к собеседованию. Расширьте свои концепции структур данных с помощью курса Python DS. А чтобы начать свое путешествие по машинному обучению, присоединяйтесь к курсу Машинное обучение - базовый уровень.

Python Машинное обучение Наука о данных

Кластеризация DBSCAN в ML | Кластеризация на основе плотности

РЕКОМЕНДУЕМЫЕ СТАТЬИ