Из Дерева Эмде Боаса | Комплект 1 | Основы и конструкция

Опубликовано: 13 Января, 2022

Настоятельно рекомендуется полностью разобраться в Дереве Прото Ван Эмде Боаса.

Дерево Ван Эмде Боаса поддерживает операции поиска, преемника, предшественника, вставки и удаления за время O (lglgN), что быстрее, чем любая из связанных структур данных, таких как очередь приоритетов, дерево двоичного поиска и т. Д. Дерево Ван Эмде Боаса работает с O (1) временная сложность для минимального и максимального запроса. Здесь N - размер юниверса, в котором определено дерево, а lg - это логарифм с основанием 2.

Примечание. Набор ключей структуры данных Van Emde Boas должен быть определен в диапазоне от 0 до n (n - положительное целое число в форме 2 ^k ), и он работает, когда дублирование ключей не допускается.

Сокращения:

VEB - это аббревиатура от дерева Ван Эмде Боаса.
ВЭБ ( 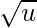) - это сокращение от VEB, содержащее количество ключей u.

Структура дерева Ван Эмде Боаса:

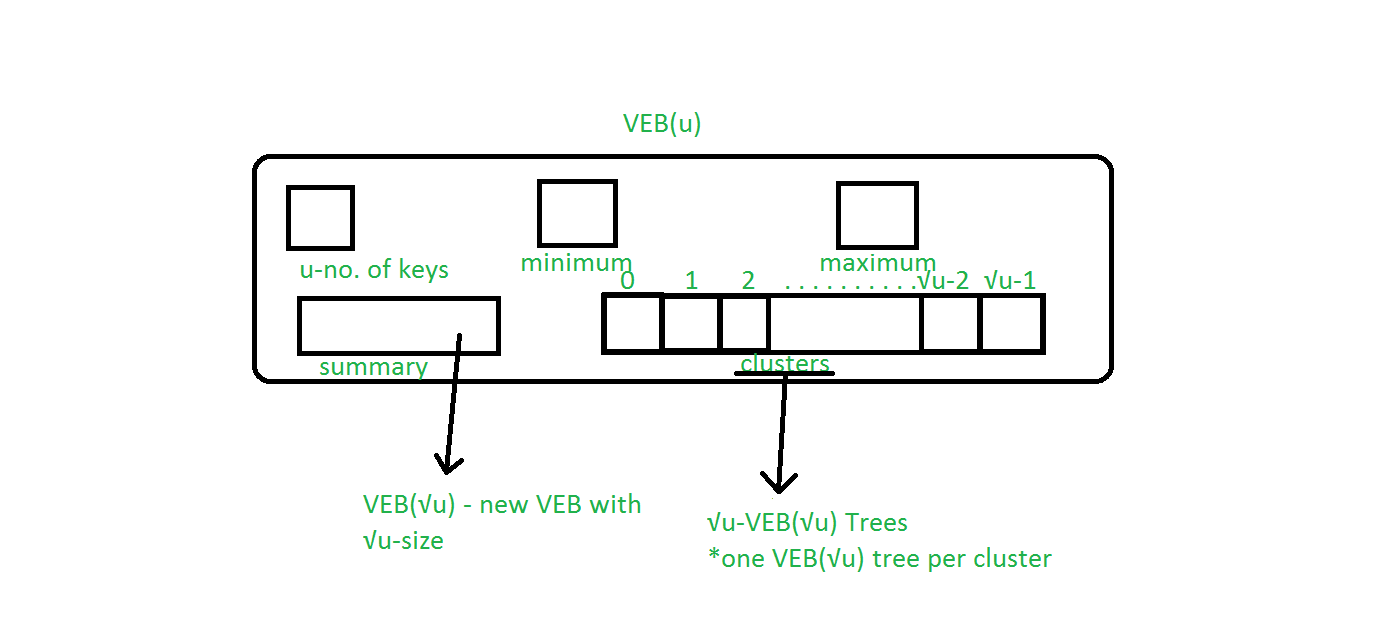
Дерево Ван Эмде Боаса - это рекурсивно определенная структура.

u : количество ключей, присутствующих в дереве VEB.
Минимум: содержит минимальный ключ, присутствующий в дереве VEB.
Максимум: содержит максимальное количество ключей, присутствующих в дереве VEB.
Резюме: указывает на новый ВЭБ ( 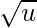) Дерево, которое содержит обзор ключей, присутствующих в массиве кластеров.
Кластеры: массив размера 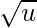каждое место в массиве указывает на новый ВЭБ ( 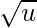) Дерево.

См. Изображение ниже, чтобы понять основы Дерева Ван Эмде Боаса, хотя оно не представляет фактическую структуру Дерева Ван Эмде Боаса:

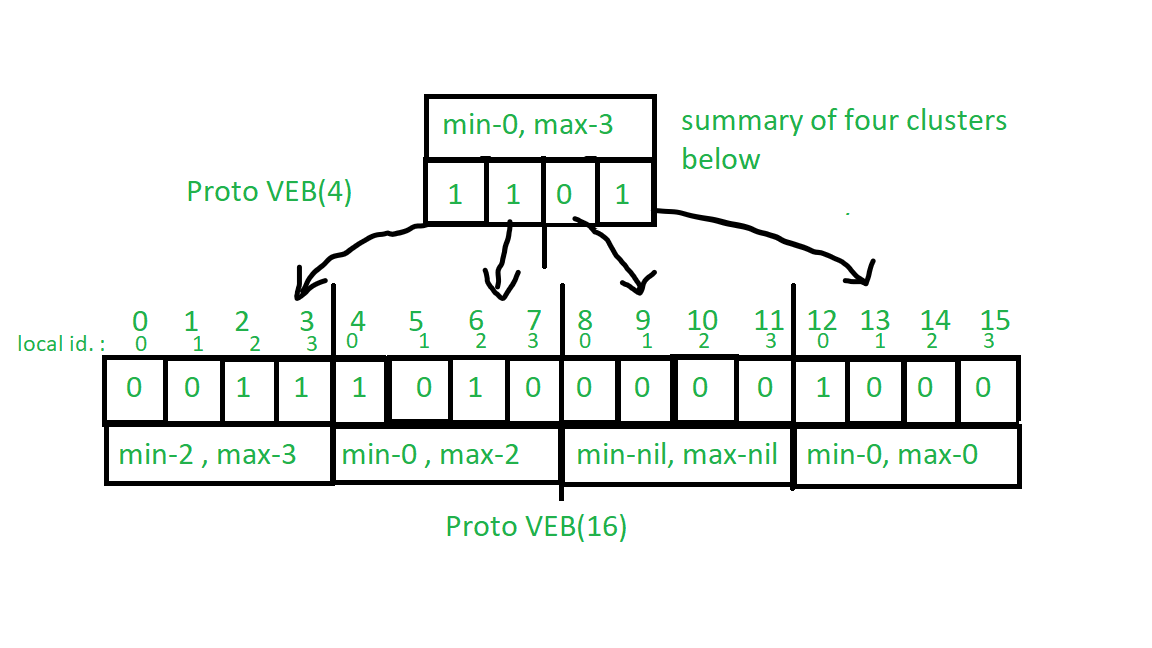
Основы понимания дерева Ван Эмде Боаса:

Дерево Ван Эмде Боаса - это рекурсивно определенная структура, аналогичная дереву Прото Ван Эмде Боаса.
В дереве Ван Эмде Боаса запросы на минимум и максимум работают за время O (1), поскольку дерево Ван Эмде Боаса хранит ключи минимума и максимума, присутствующие в древовидной структуре.
Преимущества добавления атрибутов Maximum и Minimum, которые помогают снизить временную сложность:
- Если любое из минимальных и максимальных значений дерева VEB пусто (NIL или -1 в коде), значит, в дереве нет элемента.
- Если и Минимум, и Максимум равны, то в структуре присутствует только одно значение.
- Если оба присутствуют и различны, то в дереве присутствуют два или более элемента.
- Мы можем вставлять и удалять ключи, просто устанавливая максимальные и минимальные значения в соответствии с условиями в постоянное время (O (1)), что помогает уменьшить рекурсивную цепочку вызовов: если в VEB присутствует только один ключ, то для удаления этого ключа мы просто устанавливаем min и max до нулевого значения. Точно так же, если ключей нет, мы можем вставить, просто установив min и max для ключа, который мы хотим вставить. Это O (1) операций.
- В запросах преемников и предшественников мы можем принимать решения из минимальных и максимальных значений VEB, что упростит нашу работу.

In Proto Van Emde Boas Tree the size of universe size is restricted to be of type 2^{2^k} but in Van Emde Boas Tree, it allows the universe size to be exact power of two. So we need to modify High(x), low(x), generate_index() helper functions used in Proto Van Emde Boas Tree as below.

High(x): It will return floor( x/ceil(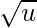) ), which is basically the cluster index in which the key x is present.
```
High(x) = floor(x/ceil())
```
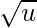Low(x): It will return x mod ceil( 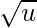) which is its position in the cluster.
```
Low(x) = x % ceil( )
```

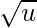generate_index(a, b) : It will return position of key from its position in cluster b and its cluster index a.

generate_index(a, b) = a * ceil(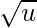) + b

Construction of Van Emde Boas Tree: Construction of Van Emde Boas Tree is very similar to Proto Van Emde Boas Tree. Difference here is that we are allowing the universe size to be any power of two, so that high(), low(), generate_index() will be different.

To construct, empty VEB: The procedure is the same as Proto VEB just two things minimum and maximum will be added in each VEB. To represent that minimum and maximum is null we will represent it as -1.

Note: In the base case, we just need minimum and maximum values because adding a cluster of size 2 will be redundant after the addition of min and max values.

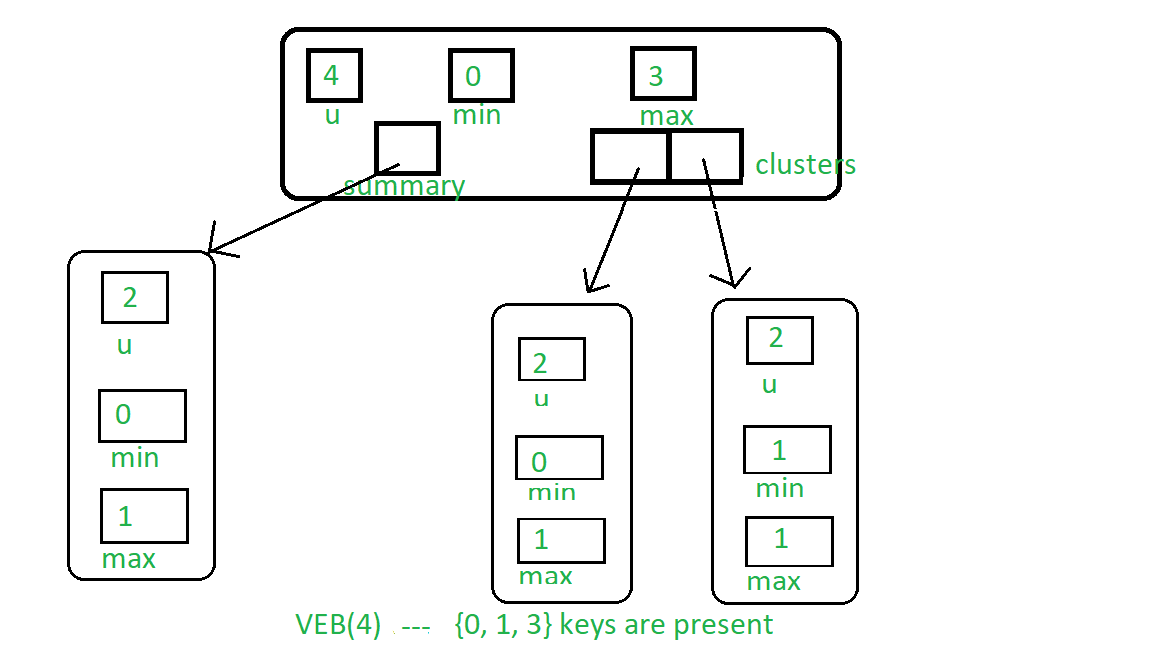
Below is the implementation:

// C++ implementation of the approach
#include <bits/stdc++.h>
using namespace std;
  
class Van_Emde_Boas {
  
public:
    int universe_size;
    int minimum;
    int maximum;
    Van_Emde_Boas* summary;
    vector<Van_Emde_Boas*> clusters;
  
    // Function to return cluster numbers
    // in which key is present
    int high(int x)
    {
        int div = ceil(sqrt(universe_size));
        return x / div;
    }
  
    // Function to return position of x in cluster
    int low(int x)
    {
        int mod = ceil(sqrt(universe_size));
        return x % mod;
    }
  
    // Function to return the index from
    // cluster number and position
    int generate_index(int x, int y)
    {
        int ru = ceil(sqrt(universe_size));
        return x * ru + y;
    }
  
    // Constructor
    Van_Emde_Boas(int size)
    {
        universe_size = size;
        minimum = -1;
        maximum = -1;
  
        // Base case
        if (size <= 2) {
            summary = nullptr;
            clusters = vector<Van_Emde_Boas*>(0, nullptr);
        }
        else {
            int no_clusters = ceil(sqrt(size));
  
            // Assigning VEB(sqrt(u)) to summary
            summary = new Van_Emde_Boas(no_clusters);
  
            // Creating array of VEB Tree pointers of size sqrt(u)
            clusters = vector<Van_Emde_Boas*>(no_clusters, nullptr);
  
            // Assigning VEB(sqrt(u)) to all of its clusters
            for (int i = 0; i < no_clusters; i++) {
                clusters[i] = new Van_Emde_Boas(ceil(sqrt(size)));
            }
        }
    }
};
  
// Driver code
int main()
{
    // New Van_Emde_Boas tree with u = 16
    Van_Emde_Boas* akp = new Van_Emde_Boas(4);
}

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with industry experts, please refer Geeks Classes Live and Geeks Classes Live USA

Структуры данных Продвинутая компьютерная тематика

Из Дерева Эмде Боаса | Комплект 1 | Основы и конструкция

РЕКОМЕНДУЕМЫЕ СТАТЬИ